Es lebe die Geometrie!

Spur des Höhen- und des
Seitenhalbierenden-Schnittpunkts

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

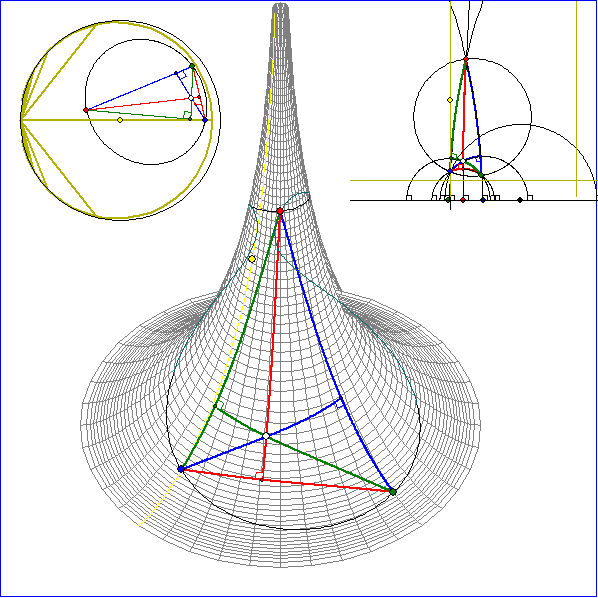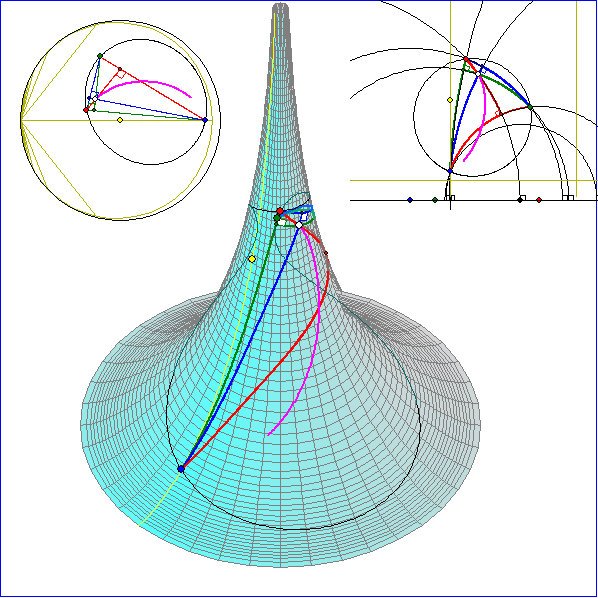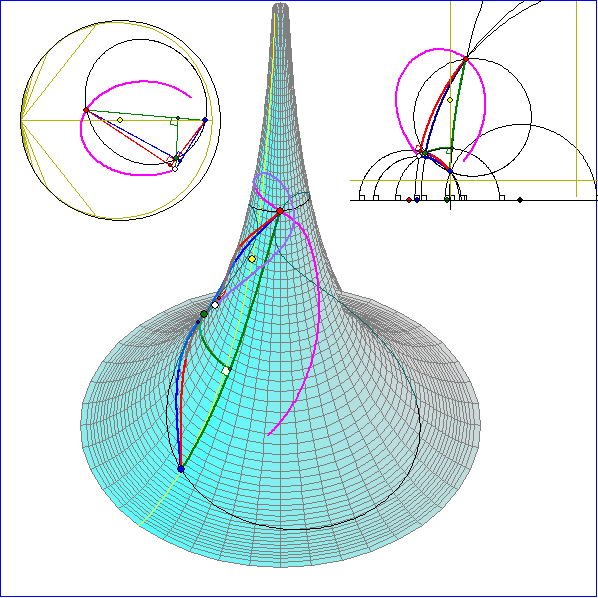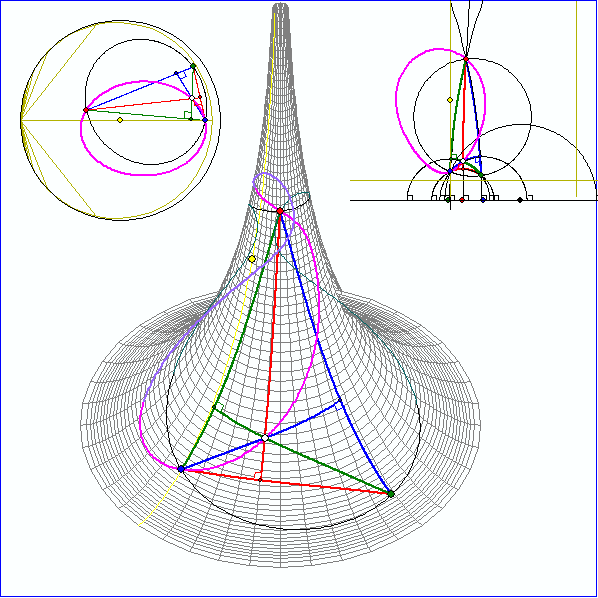
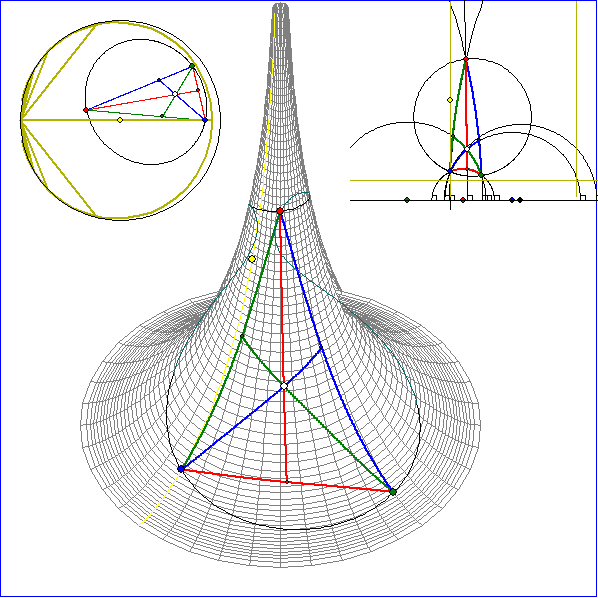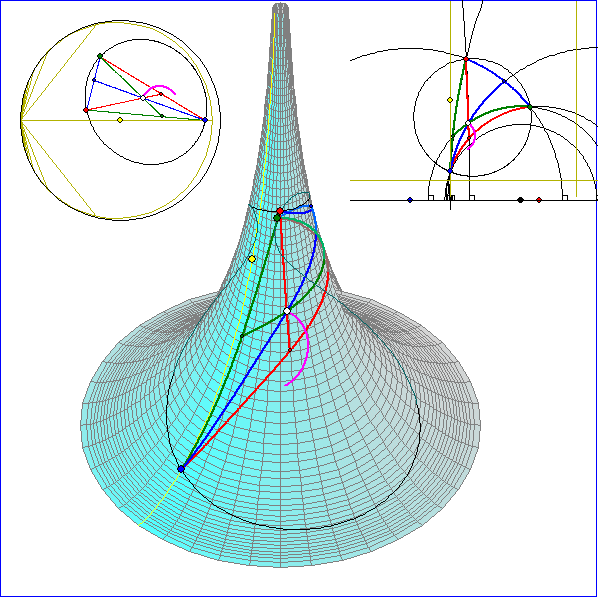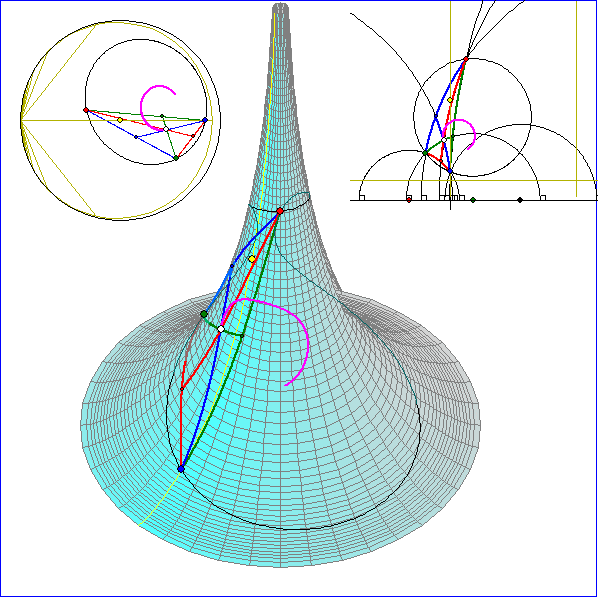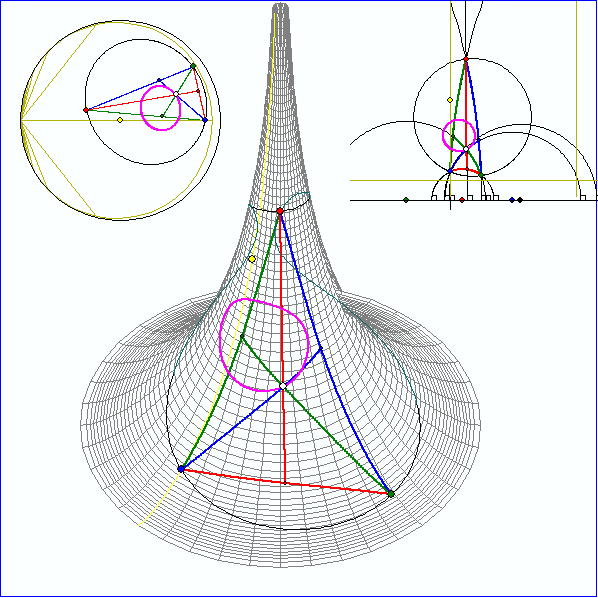
In dieser Animation wird gezeigt, dass sich in der Geometrie der Pseudosphäre auch die Höhen
eines Dreiseits in einem Punkt H schneiden. Die Spur dieses Punktes bei Drehung des Punkte G um den
geodätischen Umkreis-Mittelpunkt wird hier als magentafarbene Kurve aufgezeichnet. In der euklidischen
Geometrie ist diese Spur ein Kreis, hier aber kein geodätischer Kreis. Dies zeigt sich daran, dass das Bild
der Spur von H im Poincare-Modell oben rechts kein euklidischer Kreis ist.

Hier wird dargestellt, dass sich die Seitenhalbierenden eines geodätischen Dreiseits auf der Pseudosphäre
in einem Punkt S schneiden. Die magentafarbene Spur von S entsteht bei geodätischer Drehung von G um den
geodätischen Umkreis-Mittelpunkt.

Auch die Winkelhalbierenden haben einen Punkt gemeinsam, dessen Spur hier gezeigt wird.