Es lebe die Geometrie!

Bandwerk und Billard-Pfad

Unter einem Bandwerk verstehen wir eine Menge von endlosen Streckenzügen in der Ebene. Sie sind endlos,
weil sie entweder geschlossen sind oder weil sie sich bis ins Unendliche erstecken. Dabei sollen sich nie mehr
als zwei Streckenzüge in einem Kreuzungspunkt treffen und die Kreuzungspunkte keinen Häufungspunkt haben.
Ist P mit den Koordinaten (x ; y) Kreuzungspunkt zweier Streckenzüge, so wird er verdoppelt zu zwei Punkten
(P unten) und (P oben), die z.B. durch die Tripel (x ; y ; -1) bzw. (x ; y ; 1) beschrieben werden können
und jeweils einem der beiden Streckenzügen zugeordnet werden. An jedem Kreuzungspunkt läuft also einer
der beiden Streckenzügen über den anderen hinweg. Einen endlosen Streckenzug, dessen Kreuzungspunkte
in dieser Weise modifiziert wurden, nennen wir ein 'Band'. Zur Darstellung verwenden wir Streifen mit parallelen
Rändern, deren Mittellinie der Streckenzug ist, damit Überkreuzungen sichtbar werden.

Betrachtet werden hier nur alternierende Bandwerke mit folgender Eigenschaft: Wenn auf einem Band
zwischen Kreuzungspunkten P und Q kein weiterer Kreuzungspunkt liegt, dann überkreuzt das Band bei
P und unterkreuzt bei Q oder es unterkreuzt bei P und überkreuzt bei Q. Dieses Kreuzungsverhalten ist
bei jeder oben beschriebenen Menge endloser Streckenzüge möglich, weil zwei geschlossene Strecken=
züge stets eine gerade Anzahl von Kreuzungspunkten haben.

Im Folgenden wird stets eine durch Nachbar-Bewegungen erzeugte Kachelung zugrunde gelegt, in deren
Ausgangs-Kachel ein Streckenzug den Pfad einer Billard-Kugel angibt, die an den Seiten der Kachel
reflektiert wurde. Dieser Pfad wird durch die Nachbar-Bewegungen auf die ganze Ebene fortgesetzt.
Dabei wird verlangt, dass jede Strecke des Pfads, die mit einer Kachel-Seite einen Reflexions-Punkt
gemeinsam hat, auf der Nachbar-Kachel an dieser Seite eine geradlinige Fortsetzung findet. Start- und
Ziel-Punkt des Pfads sollen auf Kachel-Seiten liegen. Die erste und die letzte Strecke des Billard-Pfads
sollen im zugehörigen Band auf der Nachbar-Kachel so fortgesetzt werden, dass ein Winkel entsteht,
den die Seite halbiert.

Die an die ersten zehn Bilder der Gleitschau anschließenden zehn Bilder zeigen die gleichen
Bandwerke der ersten Bilder ein einer anderen Darstellung. Die folgenden zwanzig Bilder
unterscheiden sich von den ersten Bildern darin, dass der Startwinkel von 15° durch den
Startwinkel 132° ersetzt wurde. Die Folge der Bandwerke in den Sequenzen der ersten
zwanzig Bilder ergibt sich so:

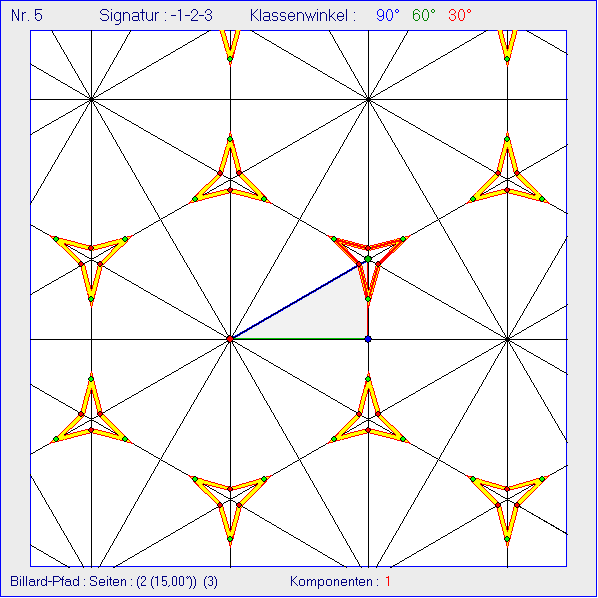
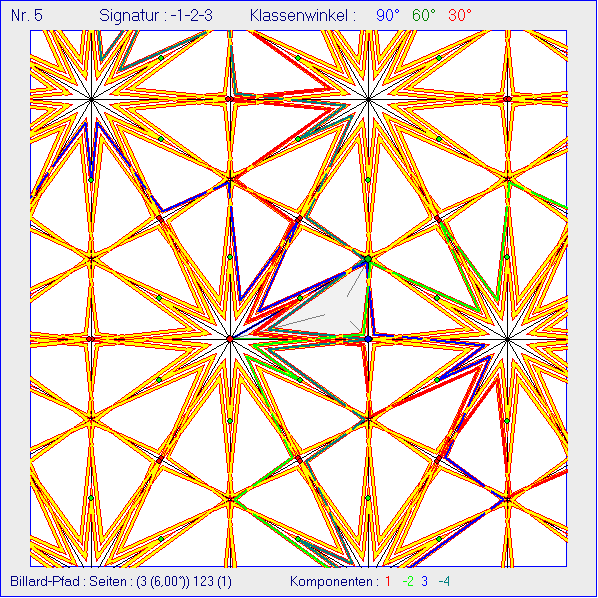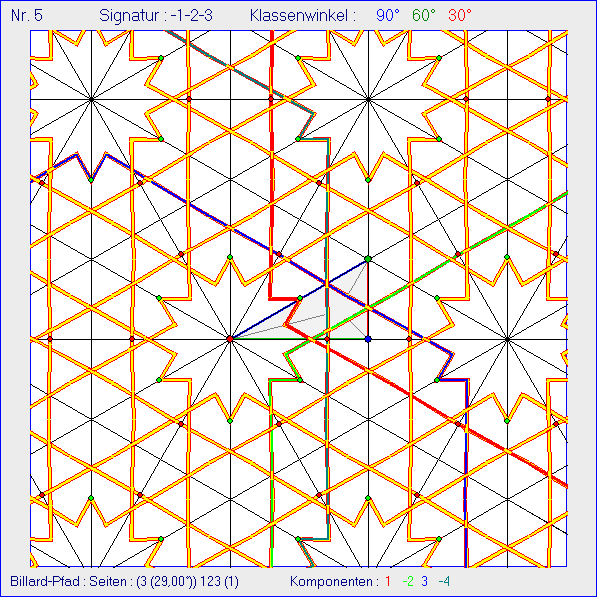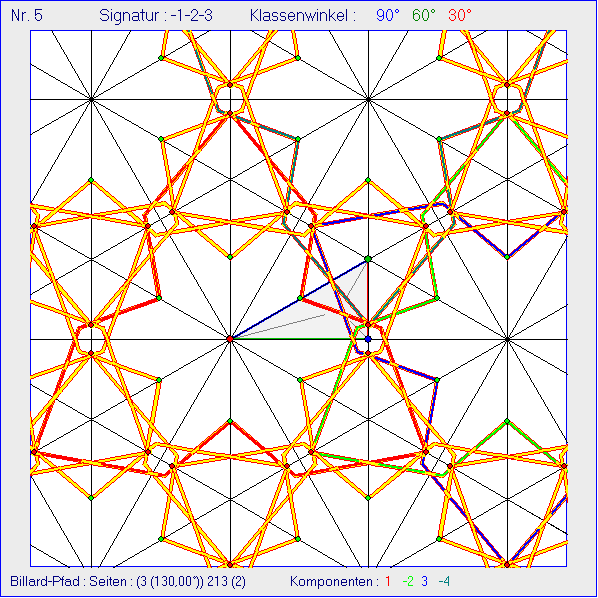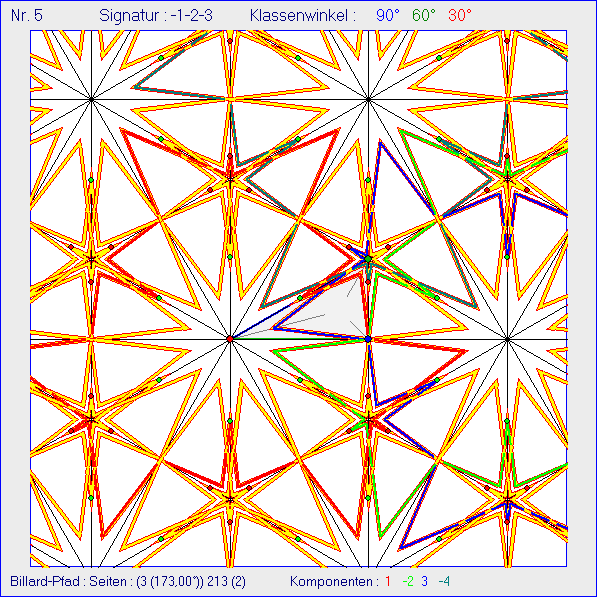
Zugrunde liegt eine Kachelung mit der farbig umrandeten Ausgangskachel K0 in der Form eines
Dreiecks mit den Innenwinkeln 90°, 60° und 30°, aus dem die übrigen Kacheln durch Spiegelung
an den Seiten entstehen. Der grüne Mittelpunkt der rot markierten Seite 2 von K0 wurde als
Ausgangspunkt eines Billard-Pfads gewählt, der unter einem Winkel von 15° gegenüber der Seite 2
startet. Im ersten Bild besteht der Pfad nur aus der Strecke von P0 bis zum ersten Refexionspunkt
einer gedachten Billard-Kugel , die sich innerhalb von K0 bewegt. Im zweiten Bild wurde der Pfad bis
zum nächsten Reflexionspunkt auf der Seite 2 weitergeführt. Dabei ergibt sich eine Menge getrennter
'Kleeblattschlingen' mit jeweils drei Kreuzungspunkten. Die Fortführung des Pfads bis zum 3. Reflexions=
punkt auf der Seite1 ergibt eine Verschlingung von sternförmigen Bändern. Die Komponenten der
Verschlingung, die K0 treffen, sind farbig unterschieden. Die Zahlen 1 -2 3 am unteren Rand des
Bildes geben in ihrem Betrag eine Nummerierung dieser Komponenten an. Das Minus-Zeichen vor 2
bedeutet, dass ein Umlauf durch die Komponente in Richtung der Billard-Strecke gegensinnig
zu den entsprechenden Umläufen auf den Komponenten 1 und 3 verläuft. Im vierten Bild mit vier
Billard-Strecken ist die Anzahl der K0 treffenden Komponenten gleich 4, erhöht sich im fünften Bild
auf 5, geht dann aber im sechsten Bild wieder auf 4 zurück. Alle Komponenten jedes so erzeugten
Bandwerks sind stets zueinander kongruent. Sie lassen sich durch einen geschlossenen Streckenzug
darstellen, bei dem alle Streckenlängen mit der Länge des Billard-Pfads in K0 übereinstimmen (vom
grünen Ausgangspunkt bis zum roten Endpunkt). Die Winkel an den grünen Eckpunkte der
Streckenzüge sind doppelt so groß wie der Startwinkel des Billard-Pfads (hier also 30°) und die an
den roten Eckpunkten doppelt so groß wie der Winkel, unter dem der Billard-Pfad beim Endpunkt
auf eine Seite von K0 trifft.

Den Auftreffwinkel kann man folgendermaßen berechnen: Es seien , und
die Richtungswinkel der Seiten von K0 gegenüber der Rechtachse bei einer Orientierung gegen den
Uhrzeigersinn. sei der Richtungswinkel der i-ten Strecke des Billard-Pfads. R(i) sei die Nummer
der Seite von K0, auf der die i-te Billard-Strecke auftrifft. Dann gilt und der
Auftreffwinkel hat die Größe .

Zum besseren Verständnis der Form der Komponenten sei die rote Komponente bei dem Billard-Pfad mit
drei Strecken betrachtet. Hier wird nacheinander an den Seiten 3 und 2 reflektiert und der rote Endpunkt
des Pfads liegt auf der Seite 1. Von grünen Startpunkt auf der Seite 2 ausgehend verläuft die rote
Komponente zunächst durch K0, dann durch die Kachel K1, die aus K0 durch Spiegelung an der Seite 3
von K0 entsteht, und dann durch die Kachel K2, die sich durch Spiegelung von K2 an deren Seite2
ergibt. Der rote Endpunkt Q der ersten Strecke von der roten Komponente liegt dann auf der Seite 1
von K2. Wir benutzen die Bezeichnung B(32) für die Bewegung, welche K0 in K2 abbildet. Wenn
die Spiegelung an der Geraden zur Seite mit der Nummer i von K0 bezeichnet, kann B(32) als Hinter=
einanderschaltung der Spiegelungen und dargestellt werden. Die Reihenfolge der Zahlen 3
und 2 erscheint also hier umgedreht. Die Strecke setzt sich zusammen aus den Strecken von nach
, von nach und von nach . Der Knick in der roten
Komponente bei Q kommt durch die Spiegelung an der Geraden durch die Seite 1 der
Kachel K2 zustande. Diese bildet die Strecke in die Strecke von Q zum grün markierten Punkt
ab. Die Bewegung B(321232) ist
eine Drehung um -60° (60° im Uhrzeigersinn), die K0 in eine Kachel abbildet, in der R die entsprechende
Lage wie in K0 hat. Die Winkelgröße -60° nennen wir darum 'Periodenwinkel' und B(321232)
'Periodenbewegung'. Aus der Ziffernfolge 321232 berechnet man die Winkelgröße durch die alternierende
Summe (Siehe dazu die Seite ' Polygon-Billard 2'). Da erst
die sechsmalige Hintereinanderschaltung von B(321232) die identische Abbildung ergibt, B(321232) also
die Ordnung 6 hat, ist die rote Komponente ein 6-zackiger Stern mit dem Drehpunkt von B(321232)
als Zentrum. Die Ziffernfolge 321232 zeigt den Zusammenhang mit der Seiten-Kennzeichnung (2) 32 (1)
des Billard-Pfads am unteren Rand der Bilder der Gleitschau.

Beim Billard-Pfad mit vier Strecken hat die entsprechende Drehung B(32131232) den Drehwinkel -120°,
die Komponenten sind 3-zackige Sterne. Bei acht Strecken hat die Drehung B(3213132123131232) den
Drehwinkel -300°. Es entstehen 12-zackige Sterne, da 12 die kleinste ganze Zahl n ist, für die
ein Vielfaches von 360° ist.

In den Bildern Nr. 3, 4, 5, 7 und 10 haben alle Komponenten wie in Bild 1 keine Überkreuzungen mit
sich selbst, da es hier eine natürliche Zahl n gibt, dessen Produkt mit dem Periodenwinkel gleich -360° ist.
In Bild 6 und 9 ist der Periodenwinkel wie in Bild 2 gleich -240°. Da hier die Gleichung
als kleinstmögliche natürliche Lösungen n = 3 und m = 2 hat, sind die Komponenten Kleeblattschlingen.
In Bild 8 hat jede Komponente 48 Kreuzungspunkt mit sich selbst.

Zur Klärung des Zusammenhangs zwischen den Periodenbewegungen der Komponenten sei wieder der
Billard-Pfad mit drei Strecken betrachtet. Die grüne Komponente, welche die zweite Strecke des Pfads
enthält, entsteht aus der roten Komponente zur ersten Strecke durch Spiegelung an der Seite 3 von K0.
Ihre Periodenbewegung ergibt sich aus der Periodenbewegung B(321232) der roten Komponente zu
, die Ziffernfolge ist also um eine Stelle
zyklisch verdreht. Entsprechend hat die blaue Komponente durch die dritte Strecke des Billard-Pfads die
Periodenbewegung B(123232).

Die Komponenten zum Billard-Pfad mit acht Strecken sind bemerkenswert, weil die blaue Komponente
die Kachel K0 in fünf Strecken des Billard-Pfads trifft. Dies bedeutet, dass die Periodenbewegung
B(1313212313123232) bei fünf zyklischen Drehungen der Ziffern eine Bewegung mit dem gleichen
Drehpunkt ergibt, nämlich den roten Eckpunkt von K0. Da die Drehwinkel gleich sind, stimmen auch
die Bewegungen selbst überein. Die Übereinstimmung von Bewegungen, welche die Kachelung auf sich
abbilden, kann dadurch getestet werden, dass man überprüft, ob ein innerer Punkt einer Kachel bei
beiden Bewegungen das gleiche Bild hat, denn bei dieser Kachelung können nur Eckpunkt der Kachelung
Fixpunkte einer Drehung sein, welche die Kachelung auf sich abbildet.

Die Bilder der obigen Gleitschau mit dem Startwinkel 312° zeigen Beispiele, in denen die Periodenbewegungen
Translationen statt Drehungen sind.

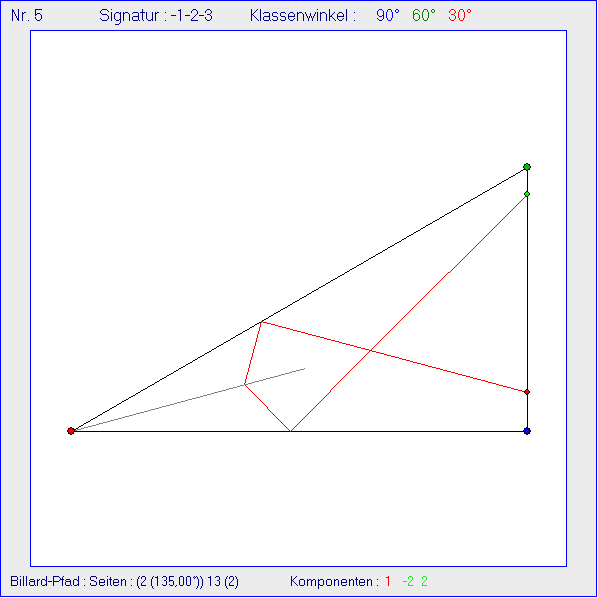
In den Bildern dieser Gleitschau ist in der Ausgangskachel eine 'Spiegelungs-Strecke' auf der
Winkelhalbierenden grau eingezeichnet, die bewirkt, dass eine Strecke des Billard-Pfads, welche die
Spiegelungs-Strecke trifft, so abknickt, dass diese zur Winkelhalbierenden des Pfads wird. Der
Richtungswinkel der ersten Strecke des Pfads beträgt 225°, also 135° gegenüber der Startseite 2.
Dabei wurden die Startpunkte variiert. Alle Komponenten sind Kleeblattschlingen.

Wegen dier 'inneren' Spiegelung muss die oben angegebene Berechnung des Auftreffwinkels an den roten
Punkten modifiziert werden. Die Überlegungen zur Periodenbewegung lassen sich unmittelbar übertragen.

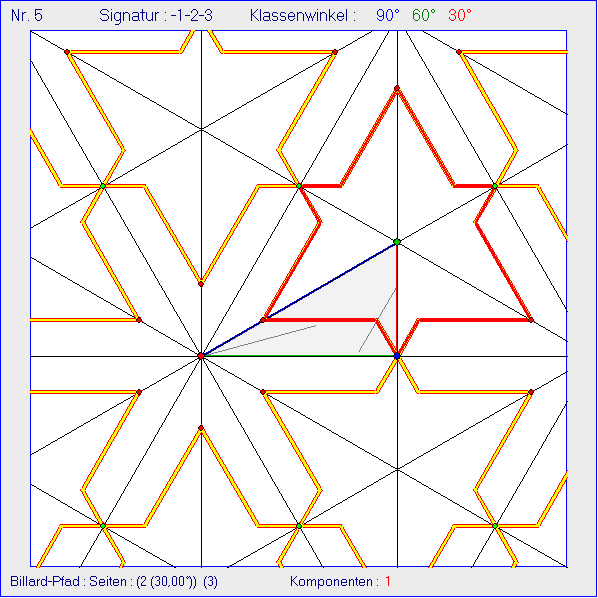
In den Bildern dieser Gleitschau sind in der Ausgangskachel zwei Spiegelungs-Strecken eingezeichnet.
Eine der beiden Spiegelungs-Strecken hat den roten Eckpunkt als Ausgangspunkt und liegt auf der
zugehörigen Winkelhalbierenden. Die zweite Spiegelungs-Strecke hat als Ausgangspunkt den Punkt,
der die rote Seite im Verhältnis teilt und damit einen Winkel der Größe 30° einschließt. In den
Bildern der Gleitschau startet der Billard-Pfad zunächst im blauen Eckpunkt mit dem Richtungswinkel
120° (30° gegenüber der roten Seite). Dabei wird die Anzahl der Reflexionen an Seiten von 0 auf 6
erhöht. Danach wird für zwei Reflexionszahlen bei gleichem Startwinkel der Ausgangspunkt auf der
roten Seite verschoben. Schließlich wird der Startwinkel auf 42,5° gegenüber dieser Seite erhöht.

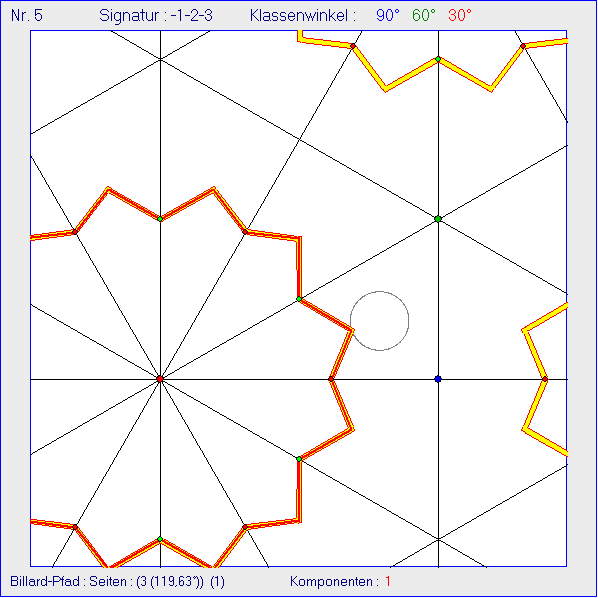
In dieser Gleitschau wird ein Billard-Pfad mit dem Startwinkel 119,63°gegenüber der Seite 3 sukzessive
verlängert. Zusätzlich zu den Reflexionen an der Seiten von K0 wird er an dem Kreis um den Inkreis-
Mittelpunkt von K0 mit dem halben Inkreis-Radius reflektiert. Die Überlegungen zur Periodenbewegung
lassen sich auch hier übertragen.

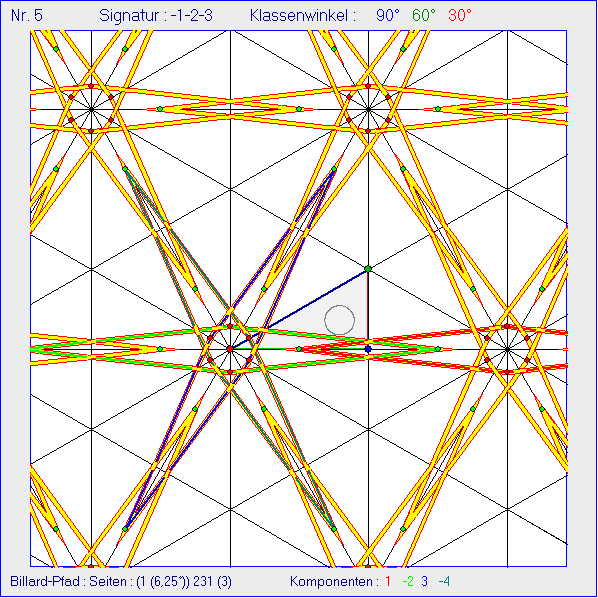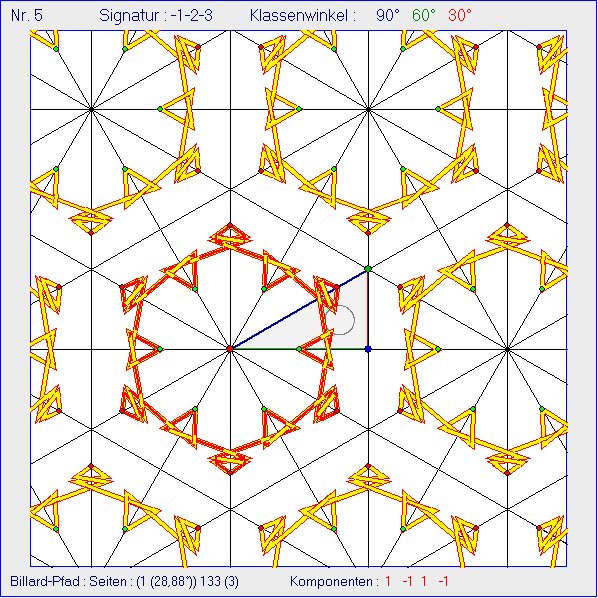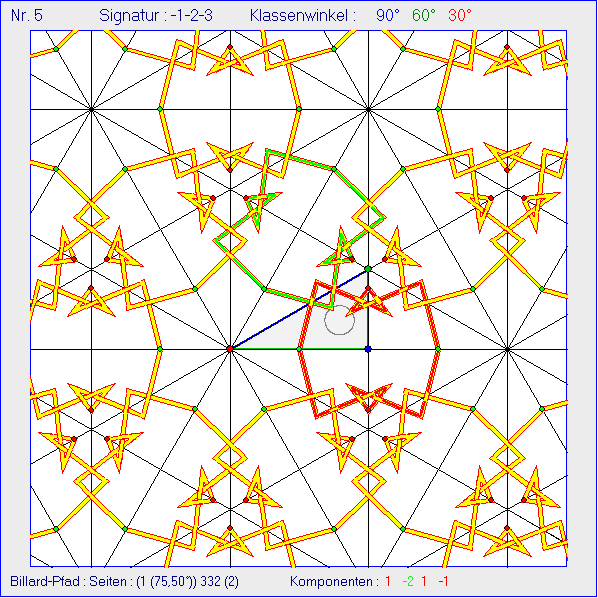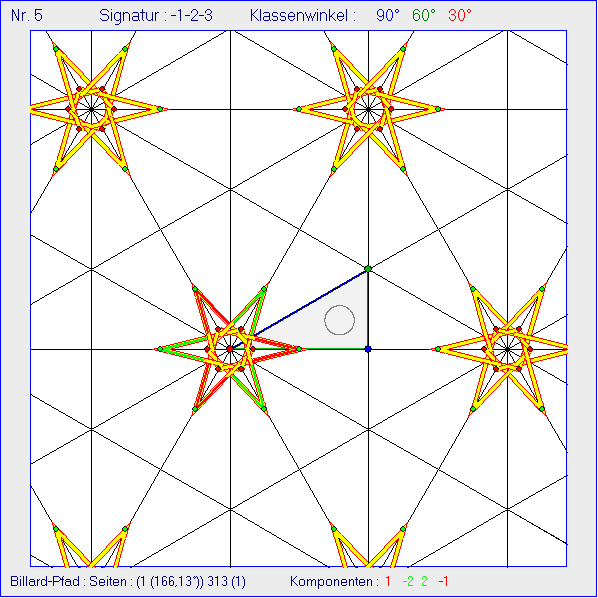
Die Gleitschau zeigt nach der Animation alle 408 Standbilder daraus. Alle Billard-Pfade in K0 haben den
gleichen grünen Anfangspunkt P0 in der Mitte der grün markierten Seite 1 von K0. Von Bild zu Bild
wächst der Startwinkel des Pfads mit der Seite 1. Seine Größe wird unten am Bildrand in Klammern
nach der Startseiten-Nummer angezeigt. Alle Billard-Pfade haben drei Reflexionen an Seiten von K0.
Zusätzlich gibt es Reflexionen an dem grau gezeichneten Kreis um das Inkreis-Zentrum von K0 mit
dem halben Inkreis-Radius.

Gegenüber der vorherigen Gleitschau wurden hier Billard-Pfade mit neun Reflexionen an Seiten
von K0 betrachtet. Nach der Animation werden daraus alle 661 Standbilder angegeben.

Hier werden die Strecken vom Inkreis-Mittelpunkt zu den Ecken im Ausgangsdreieck der Kachelung
für innere Spiegelungen benutzt. Der Billard-Pfad startet in allen Bildern auf der Seite 3 (von A nach C)
unter dem Winkel 162° gegenüber AC. In der Animation durchläuft der Startpunkt dreimal die Strecke
von C nach A und zurück. Dabei wird die Anzahl der Seiten-Reflexionen von 0 bis 5 erhöht. Die Zahl
nach 162° am unteren Rand gibt das Verhältnis des Abstands vom Startpunkt zu C und der Länge von
AC an. In der Gleitschau werden nach der Animation Standbilder daraus von den Sprungstellen des
Billard-Pfads gezeigt.

Alle hier gezeigte Billard-Pfade sind Anfangsstücke von periodischen Pfaden. Schon bei einer Seiten-
Reflexion gibt es Startpunkte, bei denen eine volle Periode durchlaufen wird, aber erst ab fünf Seiten-
Reflexionen gilt dies für alle Startpunkte auf AC. In den letzten 10 Bildern der Gleitschau werden
einige bemerkenswerte geometrische Eigenschaften der Pfade deutlich, die auf folgenden Aussagen
der Spiegelungsgeometrie beruhen:

, und seien die Spiegelungen an den Seitengeraden AB, BC und CA. , und
seien die Spiegelungen an den Winkelhalbierenden zu ABC, BCA bzw. CAB. Dann gilt für die
Hintereinanderschaltungen dieser Achsenspiegelungen:

1. für mit

2. ist Spiegelung an einer Geraden durch den Inkreis, die mit der Achse von
einen gleich großen Winkel einschließt wie die Achse von mit der von

3. ist die Spiegelung an dem Berührpunkt des Inkreises mit der Seite i.

Jede Strecke mit inneren Spiegelungen verbindet hier einen Eckpunkt mit einem Punkt auf der zugehörigen
Winkelhalbierenden, dessen Abstand vom Inkreis-Mittelpunkt halb so groß ist wie der Inkreis-Radius.
Jeder Billard-Pfad startet in der Mitte der blau markierten Seite 3 von K0 und wird dreimal an Seiten
von K0 reflektiert. Dabei wird der Startwinkel variiert.

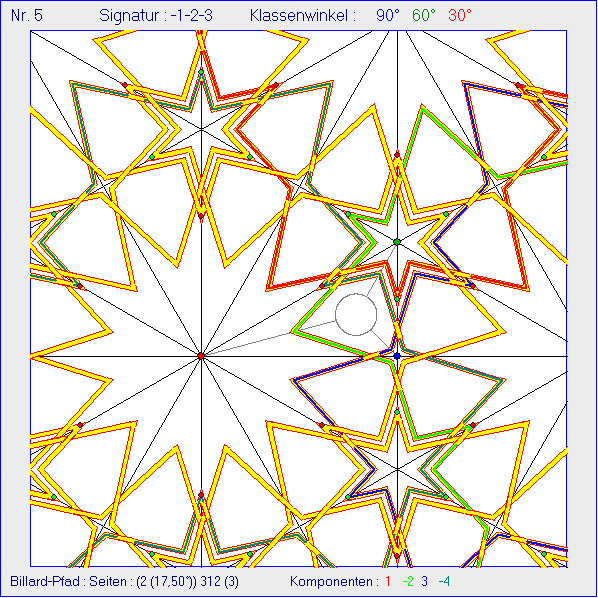
In dieser Gleischau werden die Billard-Pfade mit drei bzw. neun Seiten-Reflexionen
sowohl an dem Kreis reflektiert, als auch an den Winkelhalbierenden gespiegelt.

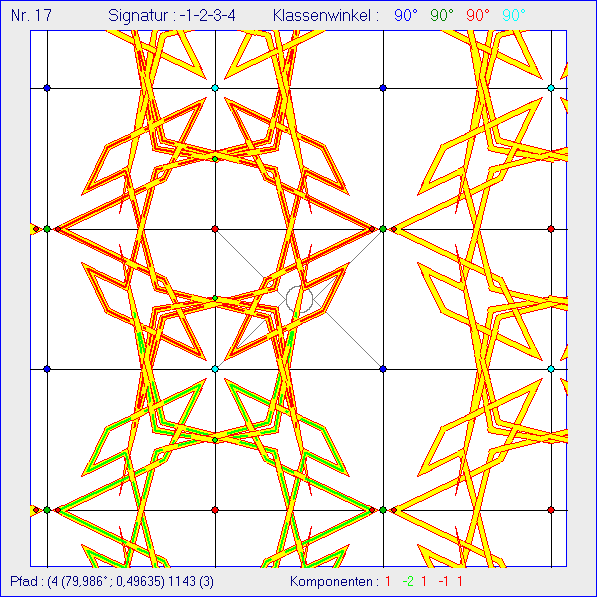
Hier wird als Ausgangskachel ein Rechteck benutzt, an dessen Seiten gespiegelt wird.
Die Billard-Pfade starten nahe der linken Seitenmitte, werden a dem grauen Kreis in der
Rechtecksmitte reflektiert und an den grauen Strecken auf den Winkelhalbierenden des
Rechtecks gespiegelt. Kleine Variationen in den Startbedingungen bewirken zum Teil
erhebliche Änderungen des Verlaufs