Es lebe die Geometrie!

Umkegelschnitte räumlicher Dreiecke, deren Eckpunkte
nullpolar zu drei Zylinder-Ellipsen sind

Die Kegelschnitte, um die es auf dieser Seite geht, entsprechen den Umkreisen von Dreiecken der
euklidischen Geometrie. A, B und C seien drei Punkte des Raumes, die drei Zylinder-Ellipsen so
zugeordnet sind, wie es auf der Seite ' Nullpolarität' beschrieben wurde. Dann gehen durch diese
Punkte viele verschiedene Kegelschnitte, die alle in der von A, B und C bestimmten Ebene liegen
und durch diese drei Punkte gehen, denn erst fünf Punkte bestimmen einen Kegelschnitt eindeutig.
Der Umkegelschnitt (kurz: Umkonik) durch A, B und C hat die besondere Eigenschaft, dass alle
Punkte darauf den gleichen Distanzmaß-Wert von einem Zentrum haben, das dem Umkreis-Zentrum
in der euklidischen Geometrie entspricht. Wir nennen es 'Zirkumzentrum'. Das Distanzmaß ergibt sich
aus der Quadratform , die den Laguerre-Spiegelungen bei Zylinder-
Ellipsen zugrunde liegt. Über die Nullpolarität führt diese Quadratform für die Quadrupel
und zweier endlicher Punkte P und Q des Raumes zu der Definition
des Distanzmaßes . Statt d(p;q) schreiben wir auch
oder d(P;Q). Von der entsprechenden Maßbestimmung der euklidischen Geometrie unterscheidet sich
dieses Maß also nur durch das Minus-Zeichen vor dem dritten Summanden. In der euklidischen Geometrie
wird aus der entsprechenden Summe von Quadraten von Koordinaten-Differenzen die Wurzel gezogen,
um den Abstand zweier Raum-Punkte zu bestimmen. Bei unserem Distanzmaß führt dies Verfahren aber
zum Teil zu rein-imaginären komplexen Zahlen, da der Maß-Wert auch negativ sein kann. Darum haben
wir bei unserer Definition auf das Wurzel-Ziehen verzichtet. Eine Addition dieser Maß-Werte hat aber
nur bei einem rechtwinkligen Dreieck ABC einen Sinn, wobei die im Folgenden erklärte Orthogonalität
zugrunde gelegt werden muss. Denn dafür gilt dann . Wenn man Strecken auf der gleichen
Geraden zusammensetzt, addieren sich höchstens die Wurzeln aus den Werte des Maßes d.

Das Zirkumzentrum wird bei diesem Distanzmaß wie in der euklidischen Geometrie durch den gemeinsamen
Punkt der Mittelsenkrechten der Dreieck-Seiten AB, BC und CA konstruiert. Der Seiten-Mittelpunkt ist
dabei der Gleiche wie beim euklidischen Abstandsmaß. Das Senkrechtstehen zweier Geraden g und h wird
durch die Orthogonalität zweier Vektoren und parallel zu g bzw. h bestimmt.
u und v sind nämlich genau dann orthogonal, wenn gleich Null ist. Diese
Orthogonalität wird in der folgenden Gleitschau durch ein doppelt gezeichnetes eckiges Winkel-Symbol markiert.

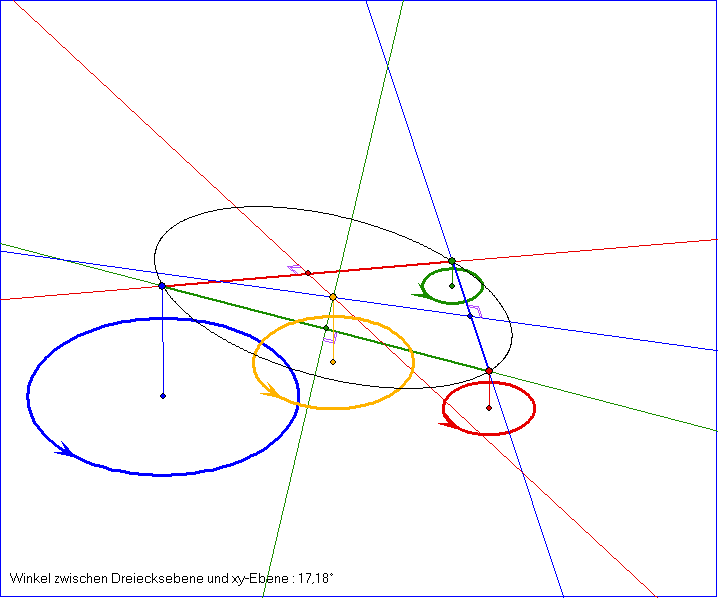
Die ersten fünf Bilder zeigen das gleiche räumliche Dreieck ABC der Kegelspitzen zu drei Zykeln, die Bilder
dreier Zylinder-Ellipsen bei der Blaschke-Abbildung sind, zusammen mit dem gelben Zirkumzentrum M, dem
zugehörigen Zykel und der schwarzen Umkonik. Im zweiten Bild sind zusätzlich gemeinsamen Tangenten
der Zykel gezeichnet. Diese haben zum Teil Schnittpunkte auf der magentafarbenen Schnittgeraden der
Dreiecks-Ebene und der xy-Ebene. Die Umkonik K ist eine nahezu kreisförmige Ellipse. Das fünfte Bild
zeigt K unverzerrt, da hier die Verbindungsgerade von Augenpunkt und Ursprung orthogonal zur Ebene von
ABC ist. In dieser Orthogonal-Projektion sind auch die folgenden 14 Bilder gezeichnet. Zuerst wird A nach
unten verschoben und in den letzten vier Bildern in Richtung der y-Achse. Dabei verändert sich der Winkel
zwischen der Ebene von ABC und der xy-Ebene. Wenn sich der Winkel 45° nähert, wird die Ellipse immer
länger und ändert sich für Winkel über 45° in eine Hyperbel.

Die Gleitschau zeigt das Dreieck ABC von Kegelspitzen dreier Zykeln mit seinem Umkegelschnitt K
in Orthogonal-Projektion.. Dieser ist eine Ellipse, da der Winkel zwischen der Ebene von ABC und
der xy-Ebene kleiner als 45° ist. Auf der Umkonik läuft der graue Punkt P herum, dessen Distanzmaß
von dem gelb-orangen Zirkumzentrum M konstant 7,70 beträgt. Für die Quadrupel
und von P und M gilt also in jeder Position auf K
.
M ist dabei Schnittpunkt der drei Mittelsenkrechten von ABC, die wie in der euklidischen Geometrie
die Mitte ihrer zugeordneten Seite orthogonal schneiden. Dabei ist der Seiten-Mittelpunkt der gleiche
wie in der euklidischen Geometrie, die Orthogonalität unterscheidet sich aber, weil für Vektoren u und v
auf der Seite bzw. der Mittelsenkrechten gilt.

Bei einem halben Umlauf von P zeigt sich neben der Distanz von M noch eine weitere Größe als konstant,
nämlich das Maß des Winkels, das in einer Halbebene von BC 96,72° beträgt und in der gegenüber
liegenden 180°-96,72°. Es überträgt sich hier also der Umfangswinkel-Satz der euklidischen Geometie.
Man berechnet dieses Winkel-Maß analog wie in der euklidischen Geometrie mit Hilfe zweier normierter
Vektoren g und h, die von P aus in Richtung B bzw. C zeigen. 'Normiert' bedeutet dabei, dass ihr
(nicht-euklidisches) Längenquadrat-Maß 1 oder -1 ist. Zum Beispiel für g wird dieses Maß mit dem Term
berechnet. Wegen des Minus-Zeichens beim dritten Summanden kann der Maß-Wert
anders als in der euklidischen Geometrie auch negativ werden. Da hier der (euklidische) Winkel zwischen
ABC-Ebene und der xy-Ebene aber kleiner als 45° ist, kommt dieser Fall hier nicht vor. Darum sind in der
Zeichung alle Vektoren grün gezeichnet und nicht auch rot wie in den folgenden Gleitschauen. Man erreicht
die Normierung eines zunächst unnormierten Vektors g, indem man die Komponenten von g durch die Wurzel
des Betrags von teilt. Wenn sowohl als auch den Wert 1 haben, hat
der Winkel BPC den Maß-Wert , wofür wir auch w(b;p;c)
schreiben. Bis auf das Minus-Zeichen im dritten Summanden entspricht das Verfahren also dem in der
euklidischen Geometrie.

In der dritten Zeile des Textes über der Zeichnung wird der Term 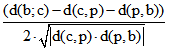betrachtet,
der offenbar wie in der euklidischen Geometrie mit -cos(w(b;p;c)) übereinstimmt. Der Kosinus-Satz kann
also auch übertragen werden. Die vierte und fünfte Zeile des Textes zeigen, dass Werte des Winkel-Maßes
sinnvoll addiert werden können. Die Abweichungen gegenüber der euklidischen Geometrie sind also sehr
klein. Eine affine Abbildung, welche die elliptische Umkonik in einen Kreis abbildet, führt jede der Figuren
der Gleitschau in eine entsprechende euklidische Figur über. Dies stimmt in den folgenden Gleitschauen nicht.

Im Unterschied zu der vorherigen Gleitschau ist hier der Winkel zwischen der Ebene von ABC und
der xy-Ebene größer als 45° mit dem Effekt, dass die Umkonik K eine Hyperbel ist. Zusätzlich zu K ist
die zu K konjugierte Hyperbel K' gezeichnet. Der Symmetriepunkt beider Hyperbeln ist auch hier
der Schnittpunkt der Mittelsenkrechten. Wie bei der Ellipse in der vorherigen Gleitschau wird die
Orthogonalität zweier Vektoren u und v auf einer Mittelsenkrechten und der zugehörigen Seiten durch
Nullsetzen der Bilinearform bestimmt. Dabei gibt es aber Vektoren v,
die zu sich selbst orthogonal sind, für die also gilt. Sie werden 'isotrop' genannt.
Sie zeigen in Richtung der Asymptoten der Hyperbeln. Isotrope Vektoren sind nicht normierbar. Darum
wird kein Wert für ein Winkelmaß w(u;v) angegeben, wenn mindestens einer der beiden Vektoren u oder
v isotrop ist. Andernfalls wird die oben angegebene Winkelmaß-Definition nur für den Fall übernommen,
dass größer als Null und der Betrag des Terms
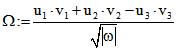kleinergleich Eins ist. Allgemein definiert man :

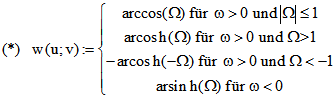
Man kann diese Definition kürzer fassen, wenn man die Integral-Darstellung
dieser Funktion für komplexe Zahlen betrachtet. Mit ist zum Beispiel ,
und . Mit der Imaginärteil-Funktion Im
ergibt sich für die Maß-Funktion w die einfachere Darstellung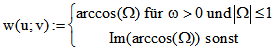


Die Distanz-Funktion d muss gegenüber der oben angegebenen Definition nicht modifiziert werden.

In der Gleitschau wird der Umfangs-Winkel BPC der Umkonik K durch die beiden normierten Vektoren
u und v von P in Richtung B bzw. C markiert. Für P auf dem oberen Hyperbel-Ast sind beide Vektoren
grün gezeichnet, weil die Terme und beide +1 ergeben, auf der unteren Hyperbel
sind sie rot, da beide Werte gleich -1 sind. In jedem Fall ist also . Wegen der Normierung von u und v
ist . Dieser Wert ist (gerundet) gleich 1,9678 oder -1,9678, je nachdem auf
welcher Seite der Geraden BC sich P befindet. Darum ist die zweite bzw. dritte Zeile der Definition (*)
anzuwenden mit dem Ergebnis 1,2982 = 74,38° bzw. -74,38°. Für P auf der zu K konjugierten Konik K'
haben u und v zu Teil eine unterschiedliche Färbung, so dass dann ist und die vierte Zeile von (*) benutzt
werden muss. Während aber für Punkte auf K der Betrag des Winkels konstant ist, gilt dies für K' nicht.

Bemerkenswert ist aber, dass das Maß für die Strecke von P zum Symmetriepunkt M der Hyperbeln
sowohl auf K, als auch auf K' konstant ist, wobei sich die Konstanten nur im Vorzeichen unterscheiden.

Die dritte Textzeile in den Zeichnungen der Gleitschau zeigt, wie der Kosinus-Satz übertragen werden kann.
Der Term 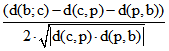stimmt nämlich hier mit cosh(w(b;p;c)) , -cosh(w(b;p;c)) oder
-sinh(w(b;p;c)) überein.

Die vierte und fünfte Textzeile in den Bildern der Gleitschau zeigt, dass es auch für die Zusammensetzung
von Winkeln eine Additionsregel gibt, bei der allerdings in etwas unübersichtlicher Weise Vorzeichen
berücksichtigt werden müssen.

Im Unterschied zur vorherigen Gleitschau liegen hier die Punkte B und C auf verschiedenen Hyperbel-
Ästen von K. Das Maß des Umfangs-Winkels BPC bleibt auf K auch hier auf jeder Seite der Geraden BC
konstant, unterscheidet sich aber im Vorzeichen auf den beiden Seiten. Die Vektoren u und v, die von P aus in
Richtung B bzw. C zeigen, haben eine unterschiedliche Farbe. Also ist hier und die vierte Zeile
der Definition (*) zur Winkelmaß-Berechnung zu verwenden. ist (gerundet)
gleich 0,7995 oder -0,7995. Darum ist w(b;p;c) = 0,7323 = 41,96° oder -41,96°.

Auf K ist stets 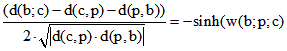, unabhängig von den Seiten von BC.
Auf K' muss zum Teil sinh durch cosh ersetzt werden.

Dieses Bild zeigt, wie sich Satz über die Euler-Gerade der euklidischen Geometrie auf den Raum der
Kegelspitzen von Zykeln übertragen lassen, die über die Blaschke-Abbildung den Ellipsen auf einem
Zylinder zugeordnet sind. Das graue Bary-Zentrum S ist der Schnittpunkt der Seitenhalbierenden,
das hellgrüne Ortho-Zentrum H der Schnittpunkt der Höhen und das gelbe Zirkum-Zentrum M der
Schnittpunkt der Mittelsenkrechten. Diese drei Punkte liegen auf der Euler-Geraden. Dabei ist
und der euklidische Abstand von H und S doppelt so groß wie der von S und M.

Zur Berechnung von Zirkum-Zentrum, Ortho-Zentrum und Bary-Zentrum :

Die Dreiecks-Eckpunkte A, B und C seien durch Quadrupel , und
gegeben. Dann ist das Bary-Zentrum der gleiche Punkt wie in der euklidischen
Geometrie, nämlich der Punkt mit dem Quadrupel
,
oder gleichwertig , da Quadrupel
identifiziert werden, wenn sie durch Multiplikation mit einer reellen Zahl ungleich Null auseinander
hervorgehen. In der euklidischen Geometrie werden das Ortho-Zentrum und das Zirkum-Zentrum
häufig mit Hilfe von Schwerpunktskoordinaten berechnet, die mit den euklidischen Längen der
Dreieck-Seiten bestimmt werden (->'Schwerpunktskoordinaten in der Dreiecksgeometrie'
https://www.vivat-geo.de/Pdf-Dateien/Schwerpunktskoordinaten.pdf). Schwerpunktskoordinaten
sind die Zahlen, mit denen man die Quadrupel , und
multipliziert, um das gewünschte Quadrupel zu erhalten. Beim Bary-Zentrum ergibt dies also das
Koordinaten-Tripel (1 ; 1 ; 1) oder auch ein Tripel (r ; r ; r) mit . Für die Berechnung von
Ortho-Zentrum und Zirkum-Zentrum benutzt man häufig die Längen a, b und c der den Punkten A,
B und C gegenüberliegenden Seiten. Nützlich sind dabei die Abkürzungen , und . Ein Schwerpunktkoordiaten-Tripel des Ortho-
Zentrums der euklidischen Geometrie ist oder gleichwertig .
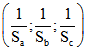Für das Zirkum-Zentrum erhält man das Tripel 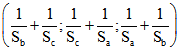. Wenn A, B und C
Kegelspitzen von Zykeln sind, für welche die Maß-Bestimmung der Laguerre-Geometrie gelten, kann
man die Tripel benutzen, die man erhält, wenn man , und durch die Distanz-Maße d(B;C),
d(C;A) bzw. d(A;B) ersetzt. Statt nimmt man also den Term
mit einem Minus-Zeichen im dritten Summanden.

Die Gleitschau zeigt, dass sich auch die Sätze über den Symmedian-Punkt Y eines Dreiecks ABC
aus der euklidischen Geometrie auf den Raum der Kegelspitzen übertragen lässt, die sich mit der
Blaschke-Abbildung aus der Geometrie der Ellipsen auf einem Zylinder ergeben. Die Gerade durch
die Mitte irgendeiner Höhe von ABC und der Mitte der zugehörigen Grundseite geht durch Y. Es gibt
auch einen engen Zusammenhang zwischen Y und dem Baryzentrum S von ABC. (Diese beiden Punkte
sind in der Gleitschau doppelt schwarz eingekreist.) Dies zeigt sich an den Winkeln, die sich ergeben,
wenn man S und Y von einem Eckpunkt aus anpeilt. Es ist nämlich zum Beispiel und
Entsprechendes gilt auch für die anderen Eckpunkte. Zwei Punkte, welche diese Winkel-Bedingung
in allen drei Eckpunkten erfüllen, werden 'isogonal konjugiert' genannt.

Weitere Beispiele für isogonal konjugierte Punkt bekommt man folgendermaßen:

sei das Dreieck der antikomplementären Ergänzung von ABC, also das Dreieck zu dem ABC
das Seitenmitten-Dreieck ist. sei das Dreieck der Schnittpunkte der Tangenten an die Umkonik
von ABC in den Eckpunkten. Die Eckpunkte von sind in der Gleitschau farbig doppelt eingekreist.
Die Zuordnung der Punkte durch die Indizierung ist dabei so gewählt, dass zum Beispiel A von und
durch die Gerade BC getrennt wird. Dann sind und isogonal konjgiert. Die Gerade durch
Y und A geht durch , ebenfalls die Mittelsenkrechte von BC. Analoges gilt auch für B und C.

Ein Schwerpunktskoordinaten-Tripel von Y ist (d(B;C); d(C;A); d(A;B)); das von , bzw.
(-d(B;C); d(C;A); d(A;B)), (d(B;C); -d(C;A); d(A;B)) bzw. (d(B;C); d(C;A); -d(A;B)). Siehe auch
hierzu 'Schwerpunktskoordinaten in der Dreiecksgeometrie'
( https://www.vivat-geo.de/Pdf-Dateien/Schwerpunktskoordinaten.pdf).