Es lebe die Geometrie!

Laguerre-Spiegelungen 2

Auf dieser Seite soll der geometrische Zusammenhang zwischen einer Zylinder-Ellipse D, einem
Spiegelungspunkt A und dem Spiegelungsbild E von D dargestellt werden, auch hinsichtlich der
Bedeutung für die Bilder von D und E bei der Blaschke-Abbildung.

Zu der dunkelblauen Ellipse D und der hellblauen Ellipse E auf dem Zylinder wurde der magenta-
farbene Punkt A gefunden, für den die zugehörige Laguerre-Spiegelung D und E vertauscht.
bzw. sei Quadrupel der Ebene, in der D bzw. E liegt. Die
dritte Komponente kann hier auf 1 gesetzt werden, weil die Ebenen nicht parallel zur z-Achse
verlaufen. Die Matrix der Spiegelung an einem Punkt A mit dem Quadrupel ist

für Punkte-Quadrupel und die dazu transponierte Matrix für
Ebenen-Quadrupel. Dabei ist F die Maß-Matrix mit den Zahlen 1, 1, 0, -1 in der Hauptdiagonalen
und sonst Nullen, die zu der symmetrischen Bilinearform gehört.
Bei Anwendung von auf d muss man bedenken, dass das Ergebnis nicht unbedingt e sein muss,
sondern auch ein dazu proportionales Quadrupel mit einer reellen Zahl r
ungleich Null sein kann. Die Gleichung hat dann die eindeutige Lösung r = -1 und 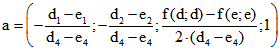. Wenn man dem Quadrupel d mit 1 als dritter
Komponente das Quadrupel zuordnet, ist a proportional zu .
Fasst man d° und e° als Punkte-Quadrupel zu Punkten D° und E° auf, teilt A die Strecke D°E° im
Verhältnis . Dabei ist der Betrag von bzw. der Radius des dunkelblauen bzw. hellblauen
Kreises in der xy-Ebene. Das Vorzeichen von bzw. legt dabei die Orientierung des Kreises fest
(linksherum Plus, rechts herum Minus). In den neun letzten Standbildern im Anschluss an die Animation
ist die Strecke D°E° braun eingezeichnet. Die Bilder zeigen die geometrische Bedeutung der Punkte
D° und E° . Zu den Zylinder-Ellipsen D und E sind die Schnittgeraden ihrer Ebenen mit der xy-Ebene
eingezeichnet. Für D ist dies die Gerade mit den Gleichungen . Die Tangenten in
den Schnittpunkten dieser Geraden mit dem Einheitskreis in der xy-Ebene schneiden
sich im Pol dieser Geraden. Ersetzt man den Einheitskreis durch die Ellipse D , dann
ergibt sich in der Ebene d entsprechend der Punkt als Pol der Geraden
bezüglich der Ellipse D. Darum ist D° der (euklidische) Mittelpunkt dieser
beiden Pole. Entsprechendes gilt für E°.

In der Animation wird der grüne Punkt P auf der dunkelblauen Zylinder-Ellipse D herum geführt und
dazu der orangefarbene Punkt Q auf der hellblauen Ellipse E. P und Q sind durch eine magentafarbene
Strecke mit dem gleichfarbigen Spiegelungszentrum A verbunden. Die zu P und Q gehörigen Pfeile der
Blaschke-Abbildung sind grün bzw. orange gezeichnet. Sie verlaufen parallel zur xy-Ebene und haben
die Länge 1. Einer der beiden gleichfarbigen Pfeile hat die Spitze bei P bzw. Q, der andere liegt in der
xy-Ebene auf einem Speer, der den Bildzykel B(D) bzw. B(E) von D bzw. E bei der Blaschke-Abbildung
berührt. Die beiden Speere schneiden sich auf der magentafarbenen Potenz-Geraden g der Kreise zu
B(D) ud B(E). Darum schneidet der magentafarbene Kreis um den Schnittpunkt der Speere beide Kreise
orthogonal in ihren Berührpunkten.

Neben der magentafarbenen Potenz-Gerade g hat auch die Gerade h durch den Ursprung und A die
gleiche Farbe. g und h sind zueinander nullpolar. Das bedeutet geometrisch, dass zu jeder Ebene
durch h eine Zylinder-Ellipse gehört, deren Blaschke-Bild ein Null-Zykel auf g ist, das heißt ein zu einem
Punkt auf g geschrumpfter Kreis vom Radius Null. Algebraisch bedeutet dies, dass die Gerade g in der
Darstellung mit Plücker-Koordinaten das Tripelpaar hat, weil das Tripel-Paar von
h ist. Darum ist g parallel zu dem Bild von h bei senkrechter Projektion auf die
xy-Ebene.Dies machen die beiden magentafarbenen Pfeile deutlich, von denen der eine seine Spitze in
einem gemeinsamen Punkt R von h und dem Zylinder hat und der andere auf g liegt. Der Punkt R liegt
auf der Ellipse jeder Ebene durch h. Darum ist das Blaschke-Bild von R ein Speer an jeden Nullzykel auf
g, muss also ganz auf g liegen. Am Ende einer Periode der Animation sind in einem Standbild zwei grau
gefüllte Pfeile vom Ursprung aus eingezeichnet, welche diesen Zusammenhang verdeutlichen. Sie sind
gleich lang, zueinander orthogonal und treffen beide senkrecht auf den Anfangspunkt des zugehörigen
magentafarbenen Pfeils.

Wir nennen die Gerade g in der xy-Ebene die 'Zykel-Achse' der Laguerre-Spiegelung
mit dem Spiegelungs-Zentrum A. Diese Zykel-Achse ist also die zur Ursprungsgeraden
durch A gehörige nullpolare Gerade.

In einem weiteren Standbild der Animation sind zwei Winkel dreifach schwarz markiert, welche die gleiche
Größe haben. Ihre Scheitelpunkte sind der Punkt S auf der z-Achse und der Schnittpunkt T der
Geraden durch die Mitten der beiden blauen Zykel und der Geraden durch die zugehörigen Kegelspitzen.
Die Gerade durch die beiden Kegelspitzen ist nullpolar zu der Schnittgeraden der Ebenen, in der die
Ellipsen D und E liegen. Der markierte Winkel links ist der Steigungswinkel der Geraden durch die Spitzen
der Kegel gegenüber der xy-Ebene. Der markierte Winkel rechts ist der Winkel zwischen der z-Achse und
der Geraden durch S und den Anfangspunkt des magentafarbenen Pfeils auf g. Die beiden Winkel liegen in
parallelen Ebenen senkrecht zu g .

Aus der Matrix M ergibt sich ein einfacher Zusammenhang zwischen den hellgrünen und orangefarbenen
Pfeilen. Denn wenn Quadupel eines Punktes P des Zylinders ist, errechnen man für
den Spiegelungs-Bildpunkt Q das Quadrupel oder gleichwertig das Quadrupel
. Die ersten beiden Komponenten beschrieben die Richtung des orangefarbenen
Pfeils. Man erhält ihn also, indem man den Pfeil durch seine Länge teilt.

Wenn man zu dem Ebenen-Quadrupel einer Zylinder-Ellipse D das Ebenen-Quadupel
der Zylinder-Ellipse E untersuchen will, das bei der Spiegelung am Punkt A mit dem
Quadupel gehört, kann man folgendermaßen vorgehen: Zunächst ist ein Quadrupel
zu E, das aber als dritte Komponente nicht 1, sondern -1 enthält. Darum setzt man . Mit den
Bezeichnungen und ist dann .
Die zu E gehörige Kegelspitze ist darum der Punkt
.
Der Mittelpunkt des Zykels zu E ergibt sich also dadurch, dass man den Mittelpunkt des Zykels zu D
mit dem Vektor senkrecht zu g beschiebt. Der signierte Radius des Zykels zu E ist dann
, wobei der signierte Radius von D ist.

Diese Animation soll den geometrischen Zusammenhang zwischen Zykeln in der xy-Ebene
und ihren Bildern bei einer Laguerre-Spiegelung klären. Dazu werden zu den Zylinder-Ellipsen
D1 und D2 (blau und dunkelrot) die Spiegelbilder E1 und E2 (hellblau und hellrot) bei der
Laguerre-Spiegelung mit dem Zentum A gezeichnet. Die zugehörigen Zykeln sind ZD1, ZD2 ,
ZE1 und ZE2. Die Zykel-Achse g ist die Potenz-Gerade der Kreise zu ZD1 und ZE1 und auch
die zu ZD2 und ZE2. Die schwarz gezeichnete Verbindungs-Strecke der Mittelpunkte MZD1
und MZE1 schneidet g senkrecht im Punkt Pg. Entsprechendes gilt für MZD2 und MZE2.
Wenn bzw. das Verhältnis vom Radius des Kreises zu ZD1 bzw. ZE1 zum Abstand von
MZD1 und MZE1 beschreibt, teilt Pg die Strecke zwischen diesen beiden Mittelpunkten im
Verhältnis .

Auf D1 und D2 werden zwei grüne Punkte P1 und P2 herumgeführt, deren Verbindungsgerade
parallel zur z-Achse verläuft. Darum gilt dies auch für die Bildpunkte Q1 und Q2 bei der Spiegelung.
Die Pfeile parallel zur xy-Ebene von einem Punkt der z-Achse zu P1 bzw. P2 bzw. Q1 bzw. Q2
sind ebenfalls grün bzw. orange, und auch deren Bilder BP1 bzw. BP2 bzw. BQ1 bzw. BQ2 in der
xy-Ebene bei der Blaschke-Abbildung. Diese Pfeile gehören zu Speeren tangential zu ZD1 bzw.
ZD2 bzw. ZE1 bzw. ZE2, die sich paarweise auf der Achse g schneiden. Wenn P1 und P2 in
einem der beiden Schnittpunkte von D1 und D2 zusammenfallen, sind auch BP1 und BP2 gleich, so
dass folglich der zugehörige Speer sowohl ZD1 als auch ZD2 berührt. Da dann auch Q1 und Q2
zusammenfallen, gehört BQ1 = BQ2 zu einem Speer tangential zu ZE1 und ZE2. In der Animation
sind in dieser Position die beiden magentafarbenen Kreise um den Schnittpunkt der beiden Speere
auf der Achse gezeichnet, die ZD1 und ZE1 bzw. ZD2 und ZE2 beide orthogonal schneiden. Die
Differenz der beiden Kreisradien ist der 'Tangentialabstand' sowohl von ZD1 und ZD2 , als auch von
ZE1 bzw. ZE2. Die Tangenrialabstände zweier Zykeln stimmen also mit den Tangentialabständen
ihrer Spiegelungsbildern überein. Wenn d und e die Quadrupel der Ebenen zu D und E bezeichnen,
wobei die dritte Komponente 1 sei, dann wird das Quadrat des Tangentialabstands durch den schon
auf der vorangehenden Seite benutzten Term

beschrieben.

Die Animation macht deutlich, wie man das Bild eines Zykels ZD2 bei der Laguerre-Spiegelung zeichnen
kann, wenn ein Zykel ZD1 zusammen mit seinem Bild ZE1 und der Achse g gegeben sind. Man legt von
irgendeinem Punkt P auf g aus einen Speer tangential an ZD2 und verschiebt ihn parallel unter Beachtung
der Orientierung bis zur Berührung mit ZD1. Vom Schnittpunkt des verschobenen Speers mit g aus legt
man den Speer tangential an ZE1 und verschiebt diesen nach P zurück. Wenn P die Punkte von g
durchläuft, hüllen die nach P zurückgeschobenen Pfeile den Bildzykel von ZD2 ein.

Bemerkenswert ist bei diesem Verfahren, dass es ausgehend von jedem Paar von orientierten Kreisen
mit verschiedenem Zentren funktioniert, wenn man die Potenzgerade g bestimmt hat. Anders als bei
den euklidischen Spiegelungen sind die Radien von Kreis und Bild-Kreis bei der Laguerre-Spiegung ja
nicht notwendig gleich.