Es lebe die Geometrie!

Pentagramma mirificum

Das Pentagramma mirificum, das sonderbare Pentagramm, ist ein Pentagramm aus fünf Großkreis-Bögen,
die an den Ecken rechtwinklig zusammentreffen. Seltsamerweise ist dies nicht nur bei einem regelmäßigen
Pentagramm möglich. Bei der von John Napier (1550-1617) angegebenen Konstruktion geht man von
einem beliebigen rechtwinkligen Großkreisbogen-Dreieck mit zwei spitzen Winkeln aus, auf dessen Seiten es
keine zwei Punkte gibt, die sich zu einem Großkreisbogen-Dreieck mit drei rechten Winkeln ergänzen lassen,
das 'Polar-Dreieck' genannt wird. Dies bedeutet für ein Großkreisbogen-Dreieck auf der Einheitskugel, dass
die Bogenlängen kleiner als sind. John Napier hat ein Verfahren entdeckt, mit einer Art modifizierter
Punktspiegelung aus dem rechtwinkligen Dreieck vier weitere zu konstruieren, die sich zu einem Kranz um
das Fünfeck der Hypotenusen zusammenschließen. Dies wird in den folgenden Animationen dargestellt.

Im Poincaré-Modell ergibt sich das reguläre Pentagramma mirificum aus dem regelmäßigen Großkreis-
Fünfeck mit den Eckpunkten durch Verlängerung der
Seiten zu einem überschlagenden Fünfeck. r wird dabei so bestimmt, dass sich die Verlängerungen
rechtwinklig treffen. Es ergibt sich der Wert . Die Animation zeigt
die Konstruktion von John Napier zum Ausgangs-Dreieck mit den Eckpunkten , und
.

Die Start- und Schluss-Bilder der acht Abschnitte der Animation werden mit einem Zwischen-Bild in der an
die Animation folgenden Gleitschau angegeben. Bild 1 zeigt das graue gleichschenklige Ausgangsdreieck ABC
mit einem Innenwinkel bei A und B und einem rechten Winkel bei C. Die Länge
der roten bzw. grünen Seite wird durch den Winkel bestimmt, unter dem sie von dem zugehörigen (roten bzw.
blauen) Pol aus erscheint, wenn er durch Großkreise mit den Endpunkten verbunden wird. Die Pol-Eigenschaft
ist daran erkennbar, dass diese Großkreise beide senkrecht auf die Seite treffen. Die farbig markierten
Mittelpunkte der Seitenkreise liegen auf einer Ursprungsgeraden durch den Pol im Abstand m vom Ursprung.
Der Abstand eines zugehörigen Pols vom Ursprung ist dann . Im Punkt A schließt das
Dreieck C'AB' nach Napiers Konstruktion an. Die Seiten AB und CA werden über A hinaus um die blau bzw.
grün gezeichneten Bögen AB' bzw. C'A verlängert, und zwar so weit, dass die Bögen BB' bzw. CC' von den
Polen aus unter dem Winkel 90° erscheinen. Dies wird in Bild 3 dargestellt. Der Pol des hellblau gezeichneten
Großkreis-Bogens BC' bildet dann mit B und C' ein Polardreieck mit rechten Winkeln an den Ecken. In den
Bildern 4 bis 12 wird dieser Prozess fortgesetzt und in den Bildern 13 bis 24 gemeinsam mit den zugehörigen
Antipoden-Dreiecken gezeigt.

Diese Animation wiederholt die Napier-Konstruktion für ein unregelmäßiges Ausgangs-Dreieck. An den
Winkelgrößen kann man bei den fünf grauen Eck-Dreiecken des Pentagramms einen Zusammenhang
erkennen. Dazu seien die Winkelgrößen zu einem 5-Tupel vereinigt in folgender Reihenfolge:
Länge r der roten Seite
Winkel s beim Eckpunkt zwischen roter und grüner Seite
Länge t der grünen Seite
Winkel u beim Eckpunkt zwischen grüner und blauer Seite
Länge v der blauen Seite.

Man liest folgende Größen ab oder erschließt sie:
(16° ; 78° ; 54° ; 20° ; 52°) (52° = 90° - 38° ergibt sich aus Bild 3)
(70° ; 38° ; 74° ; 78° ; 36°)
(12° ; 54° ; 20° ; 38° ; 16°)
(52° ; 74° ; 78° ; 54° ; 70°)
(36° ; 20° ; 38° ; 74° ; 12°)

Man kommt von einer Zeile zur nächsten durch die Abbildung


Bei Anwendung auf die letzte Zeile ergibt sich die erste, so dass sich die Konstruktion zyklisch schließt.
Die Begründung für diesen Abbildungsterm ergibt sich für die 3., 4. und 5. Komponente unmittelbar aus
der Konstruktion. Die 1. und 2. Komponente folgen daraus, dass mit dem aus einem Dreieck ABC
konstruierten Dreieck C'AB' ein Polardreieck BC'P entsteht, wobei P Schnittpunkt der Großkreise BC
und B'C' ist. Denn C' ist Pol von BC, da CC' die Länge 90° hat und bei C ein rechter Winkel vorliegt.
Entsprechend schließt man, dass B Pol von B'C' ist.

Wenn man auf den Großkreisen eine Orientierung festlegt, kann jedem orientierten Großkreis k ein Pol k*
eineindeutig zugordnet werden, üblicherweise der Pol von k, der links vom k liegt. Der zweite Pol gehört
zu dem Großkreis mit der entgegengesetzten Orientierung. Ist P ein Punkt, so sei P* die zugehörige Polare,
also der Großkreis, zu dem P der Pol ist. sei die Abbildung, die jedem Punkt den zugehörigen Antipoden
zuordnet und jedem orientierten Großkreis den gleichen Großkreis mit entgegengesetzter Orientierung. Dann
ist für alle Punkte und für alle Großkreise . Ein rechtwinkliges Großkreisbogen-
Dreieck der Napier-Konstruktion mit einer Orientierung gegen den Uhrzeigersinn kann durch ein 5-Tupel
(b ; A ; c ; B ; a) aus orientierten Seiten-Kreisen a, b, c und Hypotenusen-Eckpunkten A, B festgelegt
werden. Der Übergang zum nächsten Dreieck der Napier-Konstruktion kann man dann durch die
Abbildung beschreiben. Die Folge der 5-Tupel


zeigt, dass die identische Abbildung ist.

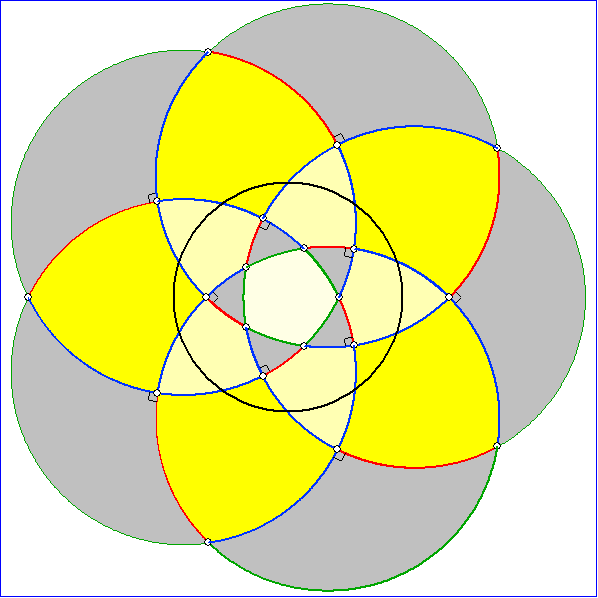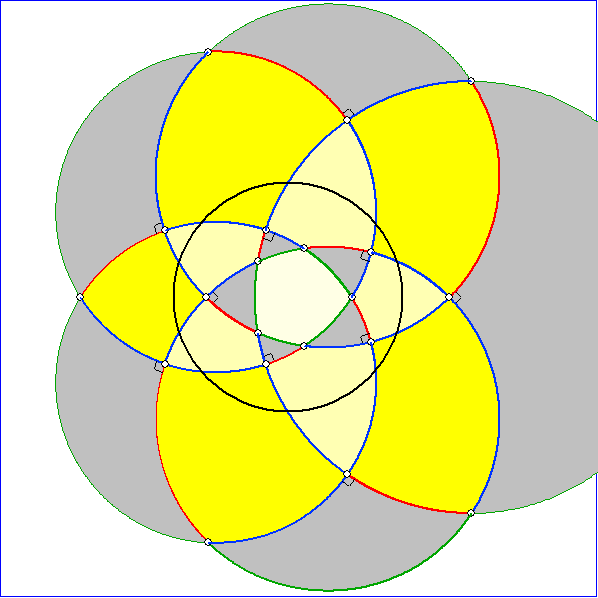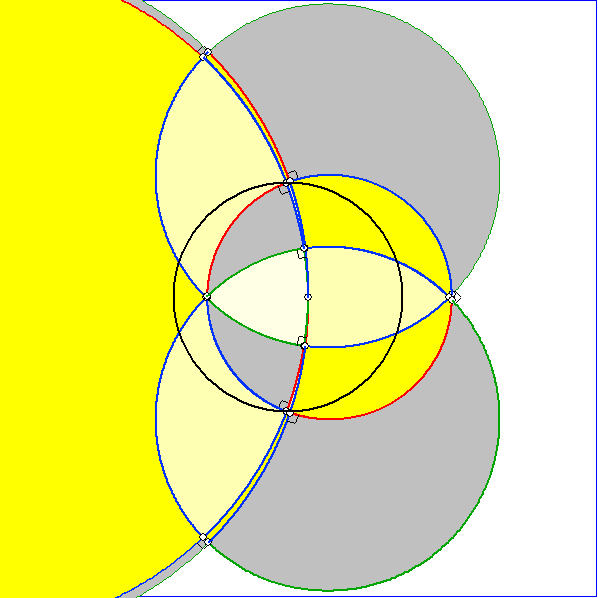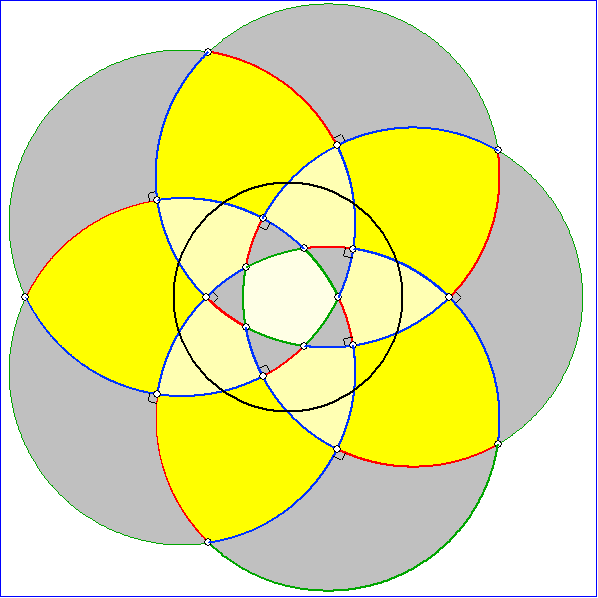
Die Animation zeigt Pentagramma mirifica mit einer Symmetrieachse und die anschließende
Gleitschau Bilder der zugehörigen Napier-Konstruktion.

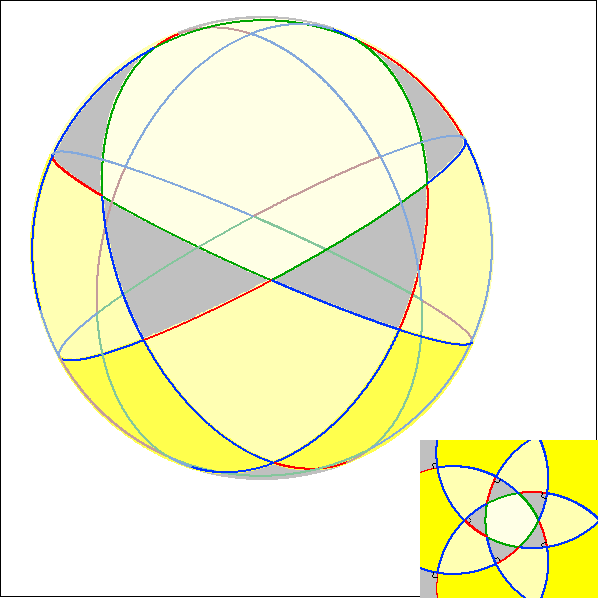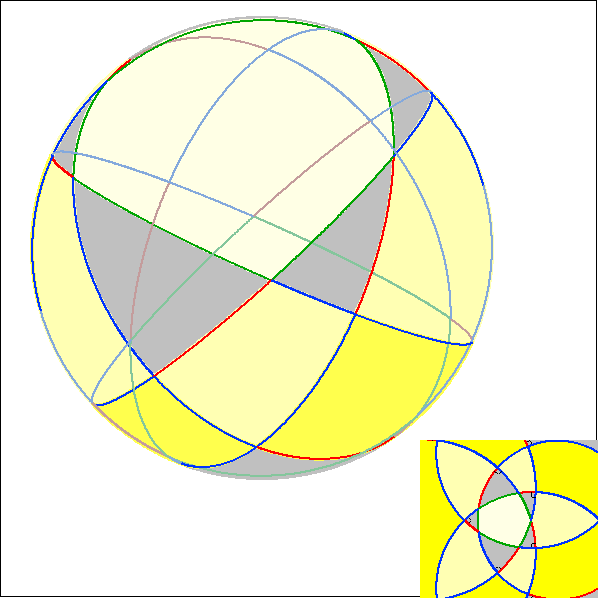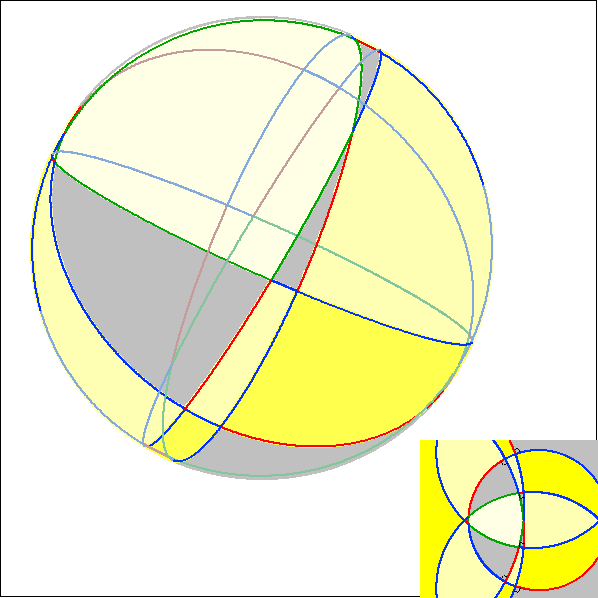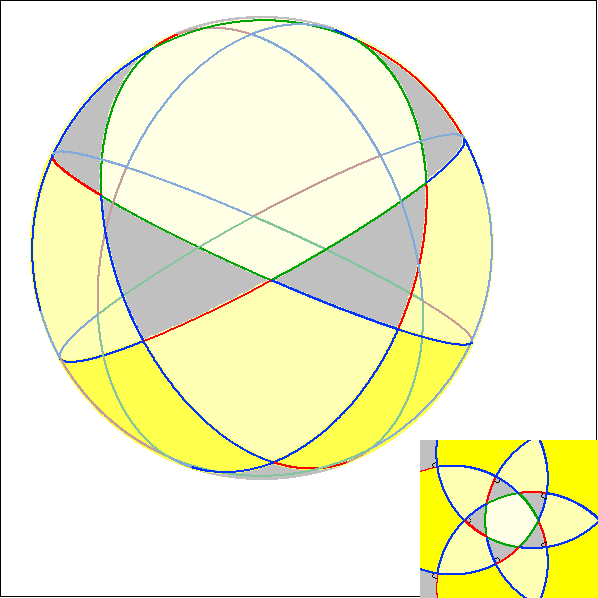
Die Animation stellt den Zusammenhang zwischen dem Pentagramma mirificum im Kugel- und im
Poincaré-Modell dar. Die Pentagramma sind im Poincaré-Modell achsensymmetrisch zur Rechtsachse.

Hier wird im Kugel-Modell das Polyeder gezeigt, das sich ergibt, indem man die Seitenbögen der
Großkreis-Polygone durch die geradlinige Verbindung der Eckpunkte ersetzt. Dieser Polyeder ist nicht
konvex, da zum Beispiel die gelben Vierecksflächen nach innen geknickt sind. Die Knick-Gerade ist
zum Teil eingezeichnet. Dass die Vierecksflächen nicht eben sind, erkennt man in Bildern der an die
Animation anschließenden Gleitschau auch daran, dass beim Kreis durch drei Eckpunkte im Poincaré-
Modell der vierten Eckpunkt im Innern liegt.