Es lebe die Geometrie!

Rotationssymmetrische Flächen, deren Gauss-Krümmung -1 ist

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

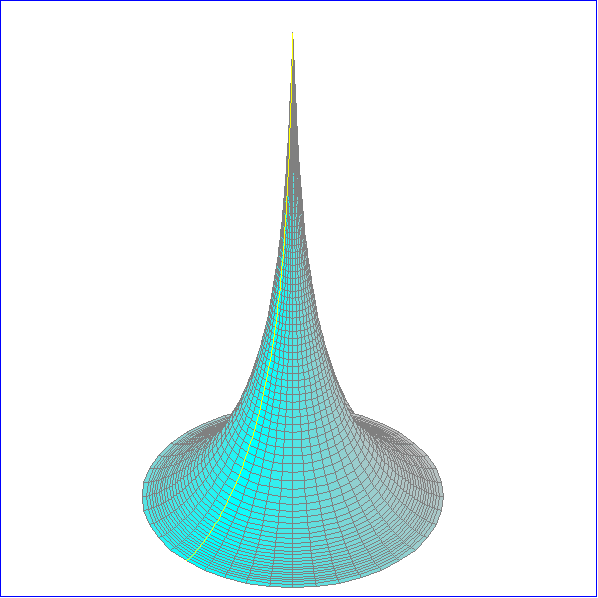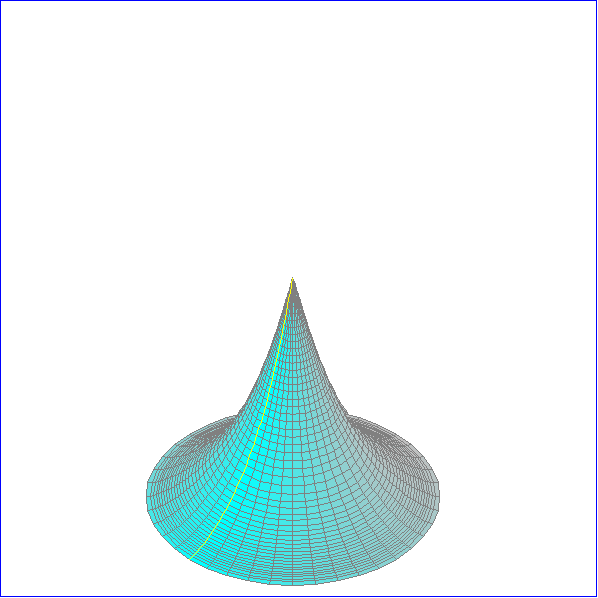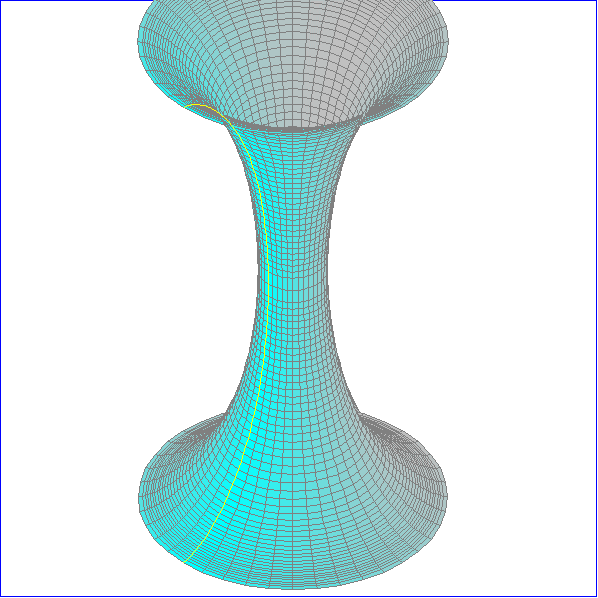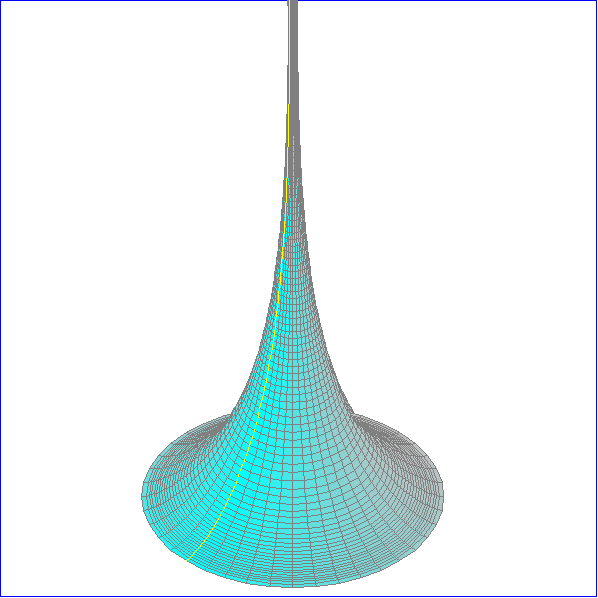
Die Animation zeigt rotationssymmetrischen Flächen, deren Gauss-Krümmung konstant -1 ist.
Sie entstehen durch z-Achsen-Rotation der Funktion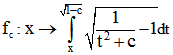

Dabei ist der Definitionsbereich das Intervall [a ; b], wobei a die größere der Zahlen -c und 0 ist
und b die obere Integrationsgrenze.Für c < 0 sind die Flächen schlauchförmig und für c zwischen
0 und 1 annähernd kegelförmig. Die obere Hälfte der schlauchförmigen Flächen entsteht durch
Spiegelung der unteren Hälfte. Für c = 0 ergiebt sich die Pseudosphäre, die durch Rotation der
Traktrix entsteht. Ferdinand Minding (1805-1885) hat 1839 bewiesen, dass jede rotationssymmetrische
Fläche mit konstanter Gauss-Krümmung -1 durch eine Funktion erzeugt werden kann.

Alle Meridiane sind Geodäten. Daneben gibt es eine zweite Art von Geodäten, die ebenfalls symmetrisch
zu einer Meridian-Ebene sind, aber nicht ganz darin liegen. Wir kennzeichnen diese Geodäten durch ein
Zahlenpaar . Dies sind die Polarkoordinaten (Abstand vom Ursprung ; Richtungswinkel) eines
Punktes in der x-y-Ebene, der durch senkrechte Projektion des Scheitelpunkts der Geodäte in die
x-y-Ebene entsteht. Dabei ist der Scheitelpunkt der Punkt der Geodäte in seiner Symmetrieebene, der einen
extremalem z-Wert hat. Die Projektion der Geodäte in die x-y-Ebenme wird dann in Polarkoordinaten
durch die Funktion 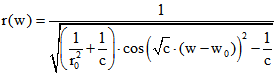beschrieben, falls c ungleich Null ist.
Wenn c kleiner als Null ist, stimmt mit überein.