Es lebe die Geometrie!

Dreiecks-Geometrie und Steiner-Zykloide

Der Gangkreis hat im Folgenden stets den Radius 1.

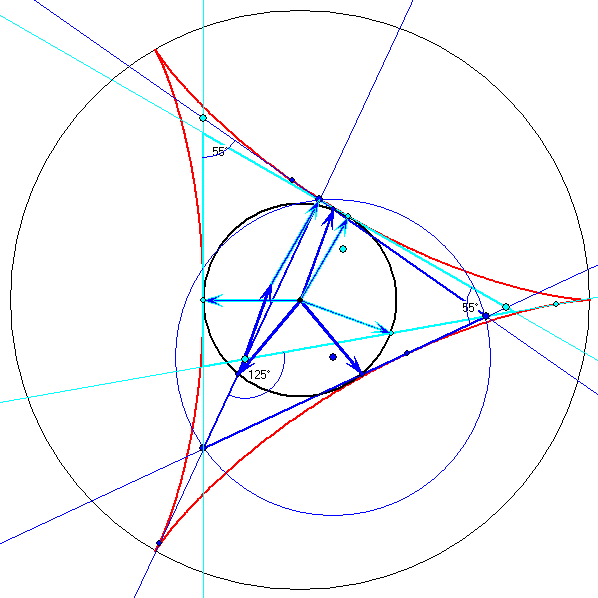
Richtungswinkel und Vektorsummen in Tangentendreiseiten
Die Bilderfolge zeigt ein dunkelblaues und ein hellblaues Dreiseit aus Tangenten der roten
Steiner-Zykloide. Die Ecken seien DEF bzw. GHJ genannt. Durch jede Ecke von DEF geht
eine Seite von GHJ. Sie ist eindeutig durch DEF festgelegt, da durch jeden Schnittpunkt zweier
Tangenten höchstens noch eine dritte gehen kann. Diese dritte Tangente schließt mit der dem
Eckpunkt von DEF gegenüberliegenden Seite einen Winkel mit der Größe ein, die für alle drei
hellblauen Geraden gleich ist. (Sorry: In der Zeichnung ist zum Teil nicht sondern die Größe
des Nebenwinkels markiert.) Wir nennen die hellblauen Geraden -Lote. ist die
Summe der Größen der Richtungswinkel von den dunkelblauen Seiten. Dabei wird nicht nur mit
identifiziert, sondern auch mit , da bei einer Geraden zwei Richtungswinkel
möglich sind, die sich um 180° unterscheiden. Wenn einen Richtungswinkel einer dieser Seiten
angibt, dann ist der Richtungwinkel des zugehörigen dunkelblauen Pfeils durch gegeben. Bei
diesem Richtungswinkel wird mit identifiziert, nicht aber mit . Die
Summe von den Richtungswinkeln der drei dunkelblauen Basis-Pfeile beträgt . In aufeinander
folgenden Bildern der Slideshow sind die Richtungswinkel aller drei Seiten von DEF um konstant 4°
erhöht, also um 12°, so dass diese Dreiecke alle ähnlich sind.

Wenn drei Tangenten einen Punkt gemeinsam haben, dann ist die Summe der Richtungswinkel der
zugehörigen Basis-Pfeile 360° = 0°. Wenn darum und Richtungswinkel zweier Seiten von
DEF sind, dann ist Richtungswinkel des -Lotes durch den zugehörigen Eckpunkt.

Die Vektorsumme der Basispfeile von drei kopunktalen Tangenten ist Ortsvektor des gemeinsamen
Punktes. Darum ist der Ortsvektor eines Eckpunktes von DEF die Vektorsumme von zwei
dunkelblauen und einem hellblauen Basispfeilen.

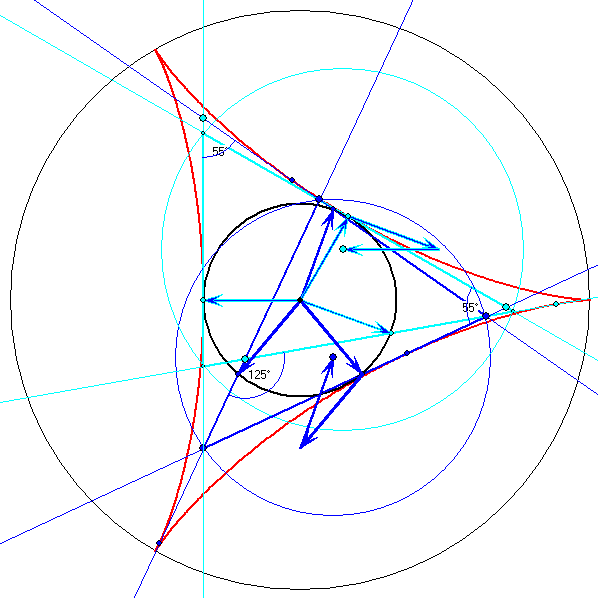
Ortsvektoren vom Umkreis-Zentrum und vom Orthozentrum
Die Vektorsumme der Basis-Pfeile der Seiten eines Tangenten-Dreiseits ist der Ortsvektor des
zugehörigen Umkreis-Zentrums. Wenn , und Richtungswinkel der Seiten sind, dann ist der
Umkreis-Radius durch gegeben. Das gilt auch für das Dreiseit
GHJ der Lote. Das Umkreis-Zentum von GHJ ist dabei der Schnittpunkt der 90°-Lote, also der
Höhen des Dreiecks DEF. Der Radius des Umkreises von GHJ beträgt .

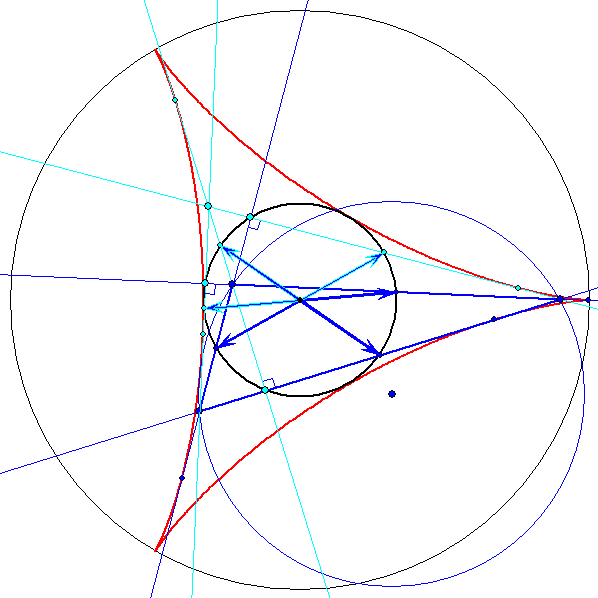
Basispfeile bei
Wenn (oder 270°) beträgt, sind die -Lote Höhen des Dreiseits DEF. Dann sind die
Basis-Pfeile der Seiten und der Höhen entgegengesetzt gerichtet. Die Spitzen der Seiten-Basis-Pfeile
sind Mittelpunkte der Seiten von DEF. Die Spitzen der Höhen-Basis-Pfeile sind die Euler-Punkte
von DEF, also die Mittelpunkte zwischen dem Orthozentrum und den Eckpunkten. Die Spitzen
aller sechs Basispfeile halbieren die Strecke zwischen einem Berührpunkt der Steiner-Zykloide
und einem Höhen-Fußpunkt. Der Kreis durch die Spitzen ist der Neun-Punkte-Kreis von DEF.

Steiner-Zykloide und Satz von Wallace
Der Satz von Wallace (manchmal auch nach Simson benannt) besagt Folgendes: Die drei Fußpunkte der
Lote von einem Punkt P des Umkreises eines Dreiecks DEF auf dessen Seitengeraden liegen auf einer
Geraden g, Wallace-Gerade genannt. Wenn H das Orthozentrum von DEF ist, dann geht g durch den
Mittelpunkt M von PH.

Bemerkenswerterweise gibt es einen Zusammenhang mit der Steiner-Zykloide: Wenn DEF ein Tangenten-
Dreiseit mit Richtungswinkel-Summe ist, dann sind die Wallace-Geraden genau die Tangenten
der Steiner-Zykloide. Dabei ist M die Basispfeil-Spitze der Tangente.

Zu den Beweisen: Salow,Edzard, Die Steiner-Zykloide, Die Wurzel, Zeitschrift für Mathematik, Juni2007
und Juli 2007