Es lebe die Geometrie!

Zusammenhang zwischen dem Klein-Modell,
dem Halbkugel-Modell und dem Poincaré-Modell

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Das Poincaré-, das Halbkugel- und das Klein-Modell sind Modelle der hyperbolischen Geometrie.

Die Punkte des Poincaré-Modells (P-Punkte) sind die Punkte (x ; y) mit y > 0 in einem kartesischen
Koordinatensystem. Die Geraden des Poincaré-Modells (P-Geraden) sind Halbkreise mit dem
Zentrum auf der x-Achse oder Halbgeraden parallel zur y-Achse. Die Winkelgrößen werden wie in
der euklidischen Geometrie bestimmt. Zu einem Halbkreis g sei C der Mittelpunkt auf der x-Achse
und S der Punkt auf g mit dem größten y-Wert. Für einen Punkt Q auf g sei die Größe des Winkels
SCQ. Dann ist der hyperbolische signierte Abstand von Q zu S durch gegeben.
Andere signierte Abstände auf g werden durch Differenzbildung daraus bestimmt.

Das Halbkugel-Modell der hyperbolischen Geometrie ist ein Zwischenglied zwischen dem Poincare-
und dem Klein-Modell. Der Graph von stellt eine Halbkugel H dar.
Die Punkte des Modells (H-Punkte) sind die Punkte dieser Halbkugel H mit dem Radius 1. Die Randpunkte
auf dem Äquator gehören nicht dazu. Die Geraden des Modells (H-Geraden) sind die Schnittkurven von H
mit Ebenen parallel zur z-Achse. Es sind dies Halbkreise, die senkrecht auf dem Äquator stehen. Die
Winkelgrößen in diesem Modell stimmen mit den euklidischen Winkelgrößen überein. Zu einer H-Geraden g
sei S der höchste Punkt und C das Zentrum des Kreises, von dem g die Hälfte ist. Zu einem Punkt Q auf g
sei die euklidische Größe des Winkels SCQ. Dann ist analog zum Poincare-Modell der hyperbolische
signierte Abstand von Q zu S durch bestimmt. Andere Abstände von Punkten auf g
ergeben sich auch hier durch Differenzbildung von signierten Abständen zu S.

Die Punkte des Klein-Modells (K-Punkte) sind die Punkte im Innern eines Kreises mit dem Radius 1.
Die K-Geraden sind die Sehnen des Kreises, wobei ihre Endpunkte keine K-Punkte sind. Die K-Punkte
und K-Geraden ergeben sich dadurch, dass die H-Punkte und H-Geraden parallel zur z-Achse auf die
x-y-Ebene projiziert werden. Die Winkelgrößen und signierten Abstände stimmen für K-Punkte und
K-Geraden mit denen für die entsprechenden H-Punkte und H-Geraden überein.

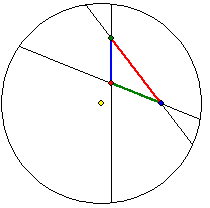
Beltrami-Klein-Modell (kurz. Klein-Modell)

Poincaré-Modell

Dieser Animation liegt ein dreidimensionales kartesisches Koordinatensystem zugrunde, in dem
die Halbkugel H mit dem Radius 1 den Graphen der Funktion darstellt.
Die Punktmenge des Poincare-Modells ist hier die Menge .
In diesem Modell ist ein Dreiseit eingezeichnet, dessen Seiten Bögen von Halbkreisen sind, die
senkrecht auf der Parallelen zur y-Achse durch den Punkt (1 ; 0 , 0) stehen. Die Eckpunkte diese
Dreiseits werden durch eine stereographische Projektion mit dem Zentrum A(-1 ; 0 ;0) auf die
Halbkugel abgebildet. Das Bild eines Eckpunkts P ergibt sich also dadurch, dass der Schnittpunkt
P' der Geraden AP mit der Halbkugel bestimmt wird. Für P = (1 ; y ; z) ist dies der Punkt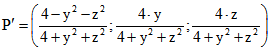
.
Der zugehörige Punkt im Klein-Modell ist der Bildpunkt von P' bei der senkrechten Projektion der
Halbkugel auf die x-y-Ebene, also der Punkt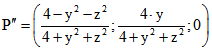
.
Bei der Untersuchung des Zusammenhangs des Klein-Modells mit der Pseudosphäre ist es sinnvoll,
in der Ebene des Poincare-Modells lokale Parameter und einzuführen mit einer
Konstanten k, z.B 0,2. Dadurch kann der Bildbereich bei der Einbettung der Riemann-Fläche der
Pseudosphäre beim Weg über das Poincare-Modell in das Klein-Modell größer oder kleiner gemacht
werden. Dem Punkt (w ; s) des Poincare-Modells ist dann der Punkt (u ; v) des Klein-Modells
zugeordnet: 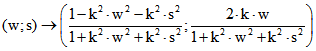. Die Umkehrabbildung ist
.

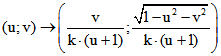Bei der stereographischen Projektion werden Halbkreise in der Ebene des Poincare-Modells in
Halbkreise auf der Halbkugelfläche abgebildet, die senkrecht auf dem Randkreis enden. Sie werden
hier H-Geraden genannt ('H' für 'Halbkugel'), Die Projektion auf die x-y-Ebene bildet diese Halbkreise
auf Sehnen des Randkreises ab.

Mit der Definitionen für die Winkelgröße und die signierten Abstände können Begriffe der euklidischen
Geometrie wie Seitenhalbierende, Winkelhalbierende, Mittelsenkrechte und Höhen auf die hyperbolische
Geometrie übertragen werden.

Die obige Animation zeigt die hyperbolische Drehung um den Schnittpunkt von H-Mittelsenkrechten eines
H-Dreiseits, bei der sich die Eckpunkte auf einem H-Kreis bewegen, der mit einem euklidischen Kreis
auf der Halbkugelfläche übereinstimmt. Die dem H-Kreis im Poincare-Modell entsprechende Figur ist
ebenfalls ein euklidischer Kreis, im Beltrami-Klein-Modell aber eine Ellipse.

Hier sind zu den Eckpunkten A, B und C eines H-Dreiseits auf der Halbkugelfläche die euklidischen
Verbindungsgeraden eingezeichnet und ihre Durchstoßungspunkte mit der x-y-Ebene. Diese Punkte liegen
auf der euklidischen Schnittgeraden g der x-y-Ebene mit der Ebene des Umkreises von ABC. Die Ebene
durch g und den Schnittpunkt M der Mittelsenkrechten im Halbkugel-Modell berührt die Halbkugel.
Die Projektion der Punkte A, B und C parallel zur z-Achse auf die x-y-Ebene ergibt das entsprechende
Dreieck im Beltrami-Klein-Modell. g ist hierbei die Polare des Punktes, der durch Projektion von M entsteht.

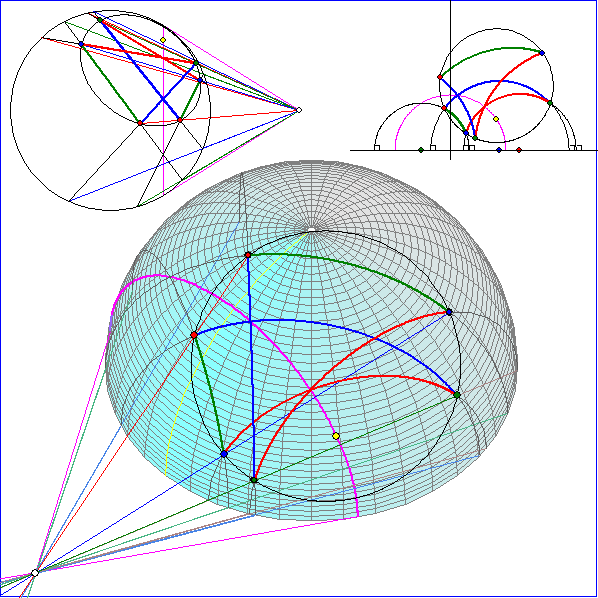
Das Dreiseit mit den Eckpunkten A, B und C im Halbkugel-Modell wird hier an der H-Geraden
g des Modells gespiegelt, die magemta-rot gezeichnet ist. Der Pol P von g ist der weiß gefüllte
Schnittpunkt der magenta-roten Tangenten an den Randkreis der Halbkugel. P ist auch der Pol
der Ebene von g bezüglich der zur Halbkugelfläche gehörenden Kugelfläche. Die Punkte A', B'
und C', die durch H-Spiegelung von A, B und C an g entstehen, sind die zweiten Schnittpunkte
der euklidischen Verbindungsgeraden von Q mit A, B und C. Die Seitengeraden des Dreiseits
werden entsprechend abgebildet, indem man die zweiten Schnittpunkte der Verbindungsgeraden
von Q mit den Enden der zu den Seitengeraden gehörenden Halbkreise auf dem Randkreis der
Halbkugel bestimmt.
Da der gelb gezeichnete H-Mittelpunkt M des Umkreises von ABC auf g liegt, geht der Umkreis
auch durch A', B' und C'. Der Pol P ist Punkt der Ebene des Umkreises und liegt auch in der
Tangentialebene von M.

Die entsprechende Konstruktion im Beltrami-Klein-Modell ist oben links angegeben. Das Bild entsteht
durch Projektion parallel zur z-Achse auf die x-y-Ebene, in der auch der Randkreis der Halbkugel
liegt.

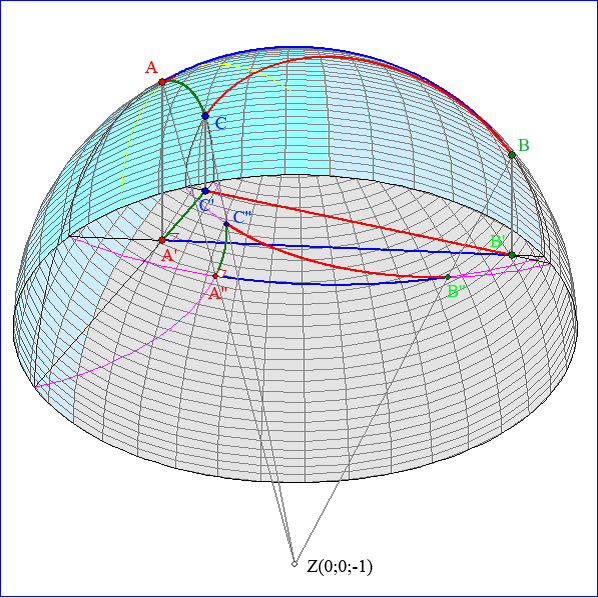
Hier sind die Halbkugelfläche-Punkte A, B und C die Eckpunkte eines Halbkugel-Dreiseits mit einem
euklidisch rechten Winkel bei A. Die Projektion parallel zur z-Achse ergibt das Dreieck A'B'C' im Klein-
Modell zu einem Dreiseit mit euklidisch geraden Strecken. Der Winkel bei A' hat in der Geometrie des
Klein-Modells die Größe 90°, ist aber kein euklidisch rechter Winkel. Die stereographische Projektion mit
dem Zentrum Z(0 ; 0 ; -1) bildet A, B und C auf ein Dreieck A''B''C'' ab, dessen Seiten Kreisbögen zu
Kreisen sind, die senkrecht auf dem Einheitskreis in der x-y-Ebene stehen. Diese Kreisbögen bilden bei A''
einen euklidisch rechten Winkel. Alle drei Winkel des K-Dreiseits A'B'C' kann man bestimmen, indem man
die euklidischen Winkelgrößen in dem Dreiseit A''B''C'' misst.
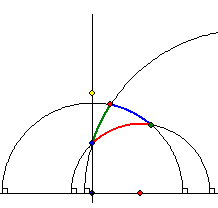
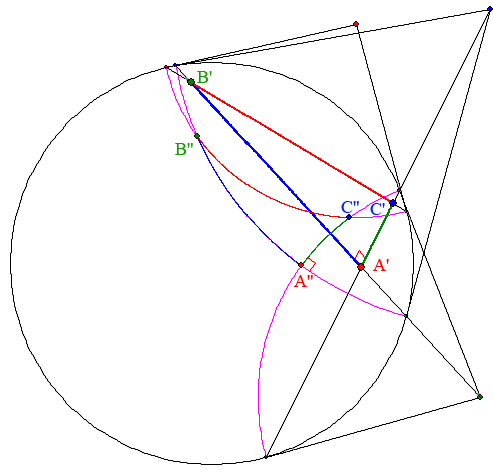
Die folgende Abbildung zeigt, wie man das Dreiseit A''B''C'' in der Zeichenebene konstruieren kann:
Man verlängert jede Seite des Dreiseits A'B'C' euklidisch geradlinig bis zum Einheitskreis und macht den
Schnittpunkt der Tangenten in den Enden zum Mittelpunkte des zu der Seite gehörenden Kreisbögens
von A''B''C''. Dieser Schnittpunkt ist der Pol der Seitengerade bezüglich des Einheitskreises.