Es lebe die Geometrie!

Drehpunktfunktion und Antikaustik
--> Erklärung zur Drehpunktfunktion (https://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf)

Drehpunktfunktion f(a) = sin(a/3)
Die dunkelblaue Drehpunktpunktkurve ist eine Kardioide (Herzkurve). Die hellblaue Spur der
Pfeilmitte E ist eine Evolvente davon. Sie ist ebenfalls eine Kardioide. Die schwarze kreisförmige
Kurve ist die Antikaustik der dunkelblauen Herzkurve bezüglich des schwarzen Punktes S. Sie
hat die Eigenschaft, dass ein Strahl, der von S ausgeht und an der Antikaustik reflektiert wird,
tangential zur dunkelblauen Kardioide verläuft. Die dunkelblaue Kardioide ist darum Kaustik des
schwarzen Kreises bezüglich S. Die Antikaustik wird mit Hilfe des pinkfarbenen gleichschenkligen
Dreiecks konstruiert mit S und der Pfeilmitte als Basis. Der Schnittpunkt A der Geraden durch den
Pfeil mit der Mittelsenkrechten zu dieser Basis liegt auf der Antikaustik. Die Mittelsenkrechte ist
Tangente der Antikaustik. Die Pfeilmitte E wird durch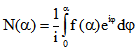
beschrieben und der Punkt A durch .
Der Punkt A teilt die Strecke von der Pfeilmitte bis zum Drehpunkt im Verhältnis 1:3.

Drehpunktfunktion f(a) = sin(a/2)
Die dunkelblaue Drehpunktpunktkurve ist eine Nephroide (Nierenkurve). Auch hier ist die hellblaue
Spur der Pfeilmitte N eine Evolvente davon. Sie ist ebenfalls eine Nephroide. Die schwarze
kreisförmige Kurve ist die Antikaustik der dunkelblauen Nierenkurve für den Fall, dass Strahlen
parallel zur Rechtsachse einfallen und an dem Kreis reflektiert werden. Der reflektierte Strahl verläuft
dann tangential zur Nephroide. Der Punkt auf dem Kreis, an dem reflektiert wird, teilt die Strecke
von der Pfeilmitte bis zum Drehpunkt im Verhältnis 1:2.

f(a) = 4
Die Drehpunktkurve ist hier zu einem Punkt D ausgeartet. Die hellblaue Spur der Pfeilmitte ist
ein Kreis um D. Die Antikaustik von D bezüglich des schwarzen Punktes S im Innern des Kreises
ist eine Ellipse, die den Kreis als Leitkreis hat.

f(a) = 6
Die Drehpunktkurve ist auch hier zu einem Punkt D ausgeartet. Die hellblaue Spur der Pfeilmitte ist
ein Kreis um D. Die Antikaustik von D bezüglich des schwarzen Punktes S außerhalb des Kreises
ist eine Hyperbel, die den Kreis als Leitkreis hat. Ein Strahl, der von S ausgeht, wird an der Antikaustik
mit einem Wechsel der Hyperbelseite reflektiert.