Es lebe die Geometrie!

Zusammenhang zwischen dem Flächeninhalt einer Drehpunktkurve
und dem Flächeninhalt einer Evolvente

-->Figuren mit konstanter Breite
https://www.vivat-geo.de/Pdf-Dateien/Gleichdick.pdf

Die Animation stellt in der ersten Periode den Zusammenhang zwischen den signierten Flächeninhalten der
Steiner-Zykloide und des Steiner-Gleichdicks (1-Kurve) dar. In den folgenden beiden Perioden werden die
s-Kurven zu s = 0,25 und s = 0,07 betrachtet. Die beiden zu vergleichende Flächen sind rechts im Bild
farbig markiert, und zwar grün bzw. rot in Flächenteilen, deren Inhalt durch eine positive bzw. negative Zahl
bewertet wird. Ein Flächenteil, der beim Durchlaufen der Randkurve mit wachsendem Richtungswinkel der
Tangente bis 360° n mal umrundet wird, geht dann mit dem n-Fachen seines Flächeninhalts im gewöhnlichen
Sinne in die Berechnung des signierten Flächeninhalts der Kurve ein. Dabei ist die 'Index' genannte Zahl n
negativ bzw. positiv, wenn die Umrundung im bzw. gegen den Uhrzeigersinn erfolgt. Je größer der Betrag von
n ist, desto dunkler ist die Färbung. Am linken Rand des Bildes sind die benutzten Farben angegeben. Das
weiße Quadrat gehört hier zu n = 0, für die Quadrate darüber nimmt der Index jeweils um 1 zu, darunter
um 1 ab.

Numerisch kann die Flächenberechnung folgendermaßen durchgeführt werden: O sei der Ursprung des
Koordinatensystems, und die Koordinaten nahe beieinander liegende Kurvenpunkte seien durch x[ i ] und
y[ i ] gegeben, wobei der Tangenten-Richtungswinkel wächst, wenn der Index i größer wird. Das Dreieck
mit O und zwei benachbarten Kurvenpunkten als Eckpunkten hat dann den Flächeninhalt
. Die Summation über alle diese Flächeninhalte ergibt dann den signierten
Flächeninhalt der zur Kurve gehörigen Fläche. Für die Steiner-Zykloide und die s-Kurve sind die Werte links
unten mit den Bezeichnungen bzw. angegeben. Diese Werte lassen sich auch in folgender Weise
deuten: Der Ortsvektor bzw. überstreicht beim Umlauf von D bzw. A um die Kurve (bis gleich
360° ist) eine Fläche, deren Inhalt dabei gemessen und aufaddiert wird, und zwar positiv bei wachsendem
Richtungswinkel des Ortsvektors und sonst negativ. Das Endergebnis nach einem vollständigem Durchlauf
der Kurve ist dann bzw. .

In dem Bild der Steiner-Zykloide in der Mitte der Animation wird diese Deutung der Flächenbestimmung für
den gelben Verbindungsvektor zwischen dem Drehpunkt D und dem zugehörigen Evolventenpunkt A
demonstriert. Dabei wird jeweils die Fläche farbig markiert, die bereits vom Vektor überstrichen wurde.
Die Farbe ist hier stets grün, weil der Richtungswinkel des Vektors der Richtungswinkel der Tangente
oder ist (im Fall s < 1), und dieser stets wächst. Wenn ein Punkt zum zweiten Mal vom Vektor
getroffen wird, verdunkelt sich der Grünton. Die Kurve, die zu der so markierten Fläche gehört, kann so
beschrieben werden: Sie führt von O ausgehend zum ersten Punkt der roten s-Kurve, durchläuft diese dann
bis zum aktuellen Punkt A an der Spitze des gelben Pfeils, geht weiter zum Anfangspunkt D des gelben Pfeils
und durchläuft dann die blaue Drehpunktkurve in Gegenrichtung bis zum Punkt O. Es zeigt sich nach einem
Durchlauf bis gleich 360° ist , dass für den so mit bestimmten Flächeninhalt gilt :
. Da sich die zugehörige Fläche aus annähernd gleichschenkligen Dreiecken
zusammensetzt mit Schenkeln der Länge , die einen kleinen Winkel einschließen, und der
Fehler für gegen Null konvergiert, kann der Inhalt durch berechnet
werden. Allgemein gilt folgender


Satz : f sei eine 1-periodische Drehpunktfunktion und s eine reelle Zahl. sei der zur
Drehpunktkurve gehörige signierte Flächeninhalt. sei der signierte
Flächeninhalt der zugehörigen s-Kurve und .
Dann gilt und .

Beweis: Auf der Seite orthogonale Figuren 1 wird gezeigt, dass
.
Eine entsprechende Formel gilt für . Denn das Lot vom Ursprung O auf die Gerade durch den Punkt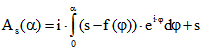
mit dem Richtungswinkel hat die Länge Darum ist der Flächeninhalt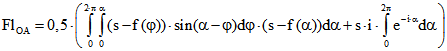

.
Wegen beweist man wie für auf der Seite orthogonale Figuren 1 , dass dann
.
Durch Auflösung der Klammern errechnet man wegen
:





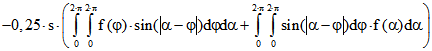
Es ist noch zu zeigen, dass . In Abhängigkeit von f ist eine Quadratform,
ebenso wie . Die zugehörige symmetrische Bilinearform ist

bzw. .
Für die Funktionen und mit ganzzahligen j, k ungleich 1, -1 und Null
und errechnet man dann . Außerdem ist ,
also unabhängig von s. Das Gleiche ergibt sich, wenn sin durch cos ersetzt wird. Für und
ist ebenfalls , auch wenn k = j ist. Da sich jede 1-periodische
Drehpunktfunktion mit dem Mittelwert Null als Grenzwert von Linearkombinationen dieser Funktionen
darstellen lässt, gilt für alle derartigen Drehpunktfunktionen . Dies gilt auch für
andere Mittelwerte, da diese nur eine Verschiebung der Kurven bewirken. Wenn man f = g setzt folgt die
Behauptung.

Speziell für errechnet man , und .
Die Formel gilt für alle Drehpunktfunktionen mit ganzzahligen k ungleich
1, -1 und Null.

Die 1-Kurve ist für kein Gleichdick, wohl aber ein Triphil. Das bedeutet, dass sich die
Kurve zwar nicht in einem Quadrat (an allen Seiten) berührend gedreht werden kann, wohl aber in einem
gleichseitigen Dreieck (siehe die Seite ' n-Phil'). Auch hier gilt aber für alle s-Kurven.
Es ist , und .

Für die Drehpunktfunktion ist die 1-Kurve ein Gleichdick, da 5 ungerade ist.
, und .