Es lebe die Geometrie!

Großkreis-Kachelung, die durch Spiegelungen an den Seiten aus
einem Kreis-Dreieck mit Winkeln 90°, 60° und 36° erzeugt wird

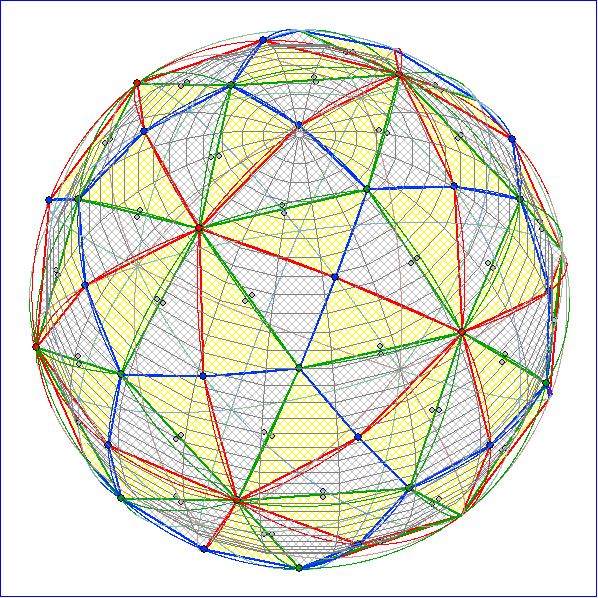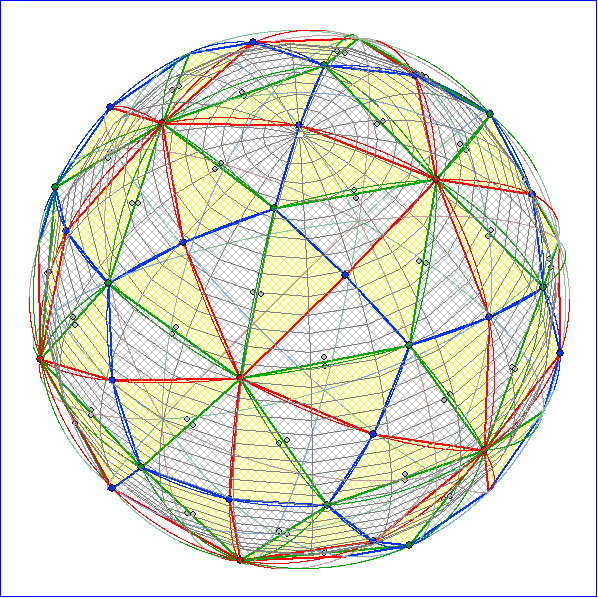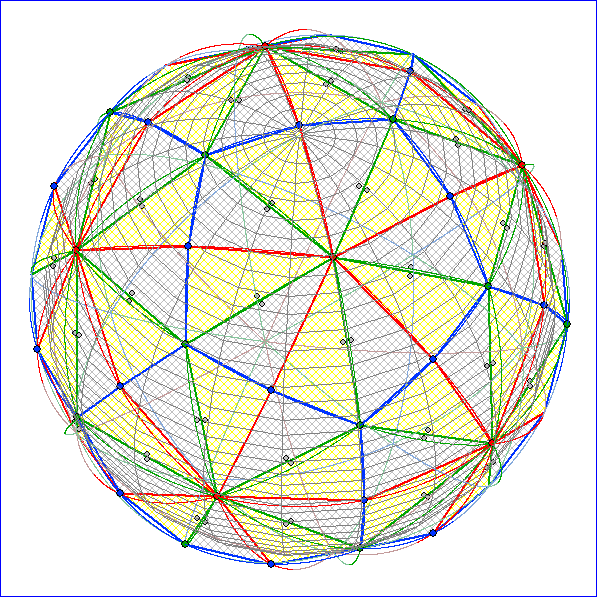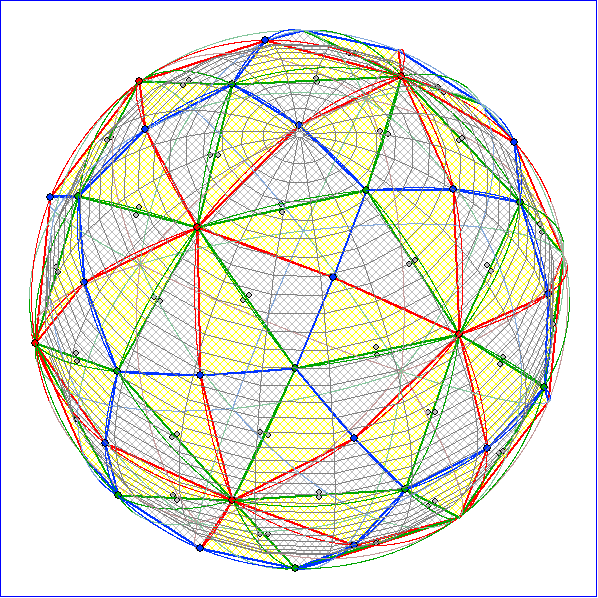
Die Großkreis-Kachelung aus Dreiecken mit den Innenwinkel-Größen 90°, 60° und 36° nennen
wir Ikosaeder-Kachelung, da die Verbindung der roten Eckpunkte mit der Nummer 1 ein Ikosaeder
ergibt (Bild 2, 3 und 4). Die grünen bzw. blauen Eckpunkte liegen dann über den Mitten der Flächen
bzw. Kanten. Bei der Verbindung der grünen Eckpunkte der Kugel-Kachelung erhält man ein
Dodekaeder mit den blauen bzw. roten Punkten über den Kanten bzw. Flächen (Bild 5 und 6). Bei
Verbindung der blauen Eckpunkte folgen die Kanten den magentafarbenen Höhen auf den grünen
Seiten. und es ensteht ein Ikosidodekaeder mit gleichseitigen Dreiecken und Fünfecken als Flächen.
Dann liegen die grünen Eckpunkte über den Dreiecken, die roten über den Fünfecken und die
Fußpunkte der Höhen über den Kanten (Bild 7 und 8). Diesen archimedischen Körper kann man
sich folgendermaßen entstanden denken: Man wendet auf das Ikosaeder in Bild 3 eine Streckung mit
dem Kugelmittelpunkt als Zentrum an, so dass die Mitte der Kanten auf die blauen Eckpunkte fallen.
Dann schneidet man die Ecken des entstandenen Ikosaeders bis zu den blauen Punkten ab. Analog
kann man beim Dodekaeder in Bild 5 verfahren.

Bild 9 zeigt das elliptische Klein-Modell der Kachelung mit eingezeichneten Höhen.

Die Animation zeigt den Aufbau der Ikosaeder-Kachelung im Poincaré-Modell und auf der Kugel.
Die Eckpunkte des Ausgangsdreiecks sind dabei
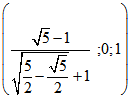, und .
Der Mittelpunkt des Kreises zur grünen Seite 2 hat die Koordinaten .

Hier wird gezeigt, dass die Teil-Kachelung im Poincaré-Modell innerhalb bzw. außerhalb des
schwarzen Kreises C von Radius 2 zu der vollständigen Ikosaeder-Kachelung im Klein-Modell gehört.

Die Spiegelung an den Seiten der Kacheln ist bei einer Konstruktion mit Zirkel und Lineal im Poincaré-
Modell zwar deutlich einfacher als im Klein-Modell, weil hier die das euklidische Winkelmaß benutzt
werden kann. Die rechnerische Darstellung der Spiegelung ist dagegen im Klein-Modell eher einfacher.
Denn sei P(x ; y ; 1) ein Punkt im Klein-Modell, der an der Geraden g mit der Gleichung
gespiegelt werden soll. Diese Gleichung beschreibt g in einem zweidimensionalen
Koordinatensystem mit dem Nordpol als Ursprung. Die Ebene G durch g und den Kugelmittelpunkt O
hat im dreidimensionalen Koordinatensystem die Gleichung . Die Gerade h durch
O und den Punkt (a ; b ; d) ist eukldisch orthogonal zu G und schneidet die Kugel in dem Punkt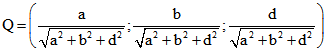
.
Wenn man die Koordinaten von Q mit dem Skalarprodukt des Ortsvektors von Q mit dem von P
multipliziert, erhält man den Ortsvektor vom Fußpunkt F des Lots von P auf h, nämlich
.
j sei die Gerade durch O und P. Das Bild k der euklidischen Spiegelung von j an G stimmt mit dem der
euklidischen Spiegelung von j an h überein, und auf k liegt der Punkt
.



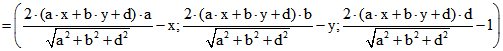
Die Division durch die dritte Komponente diese Tripels ergibt dann das elliptische Spiegelbild von P.

Durch eine ähnliche Rückführung auf die Kugel erkennt man, dass zwei Geraden im Klein-Modell mit
den Gleichungen und genau dann orthogonal sind, wenn
gilt.