Es lebe die Geometrie!

Gärtner-Methode und Drehpunkt-Funktion

Beim Anlegen von ellipsenförmigen Beeten in höfischen Gärten wurden in den Brennpunkten zwei
Pflöcke in die Erde gesetzt und ein an den Enden zusammengeknotetes Seil darumgelegt. Eine Ellipse
ergibt sich dann dadurch, dass man das Seil mit einem dritten Pflock zu einem Dreieck straff spannt
und ihn so um die beiden Brennpunkt-Pflöcke herumführt. Die beiden Dreieckseiten am dritten Pflock
schließen dann mit der Ellipsen-Tangente einen gleich großen Winkel ein (Billard-Eigenschaft). Wenn man
das Seil nicht um zwei Pflöcke, sondern um einen Zylinder mit elliptischer Grundfläche legt, ergibt sich
eine konfokale Ellipse mit der Billard-Eigenschaft. Bei anderen Formen der Grundfläche des Zylinders
erhält man zwar keine Ellipse mehr, aber die Billard-Eigenschaft der so erzeugten Billard-Kurve bleibt
erhalten. Das wird im Folgenden begründet und an Beispielen gezeigt.

Der Zylinderrand ist eine Kaustik der Billard-Kurve, d. h. wenn die erste Strecke einer Bilard-Trajektorie
tangential zum Zylinderrand verläuft, dann auch jede weitere Strecke.


Um den Rand der Grundfläche des Zylinders zu zeichnen, benutzen wir eine Drehpunkt-Funktion f. Sie
ordnet jedem Richtungswinkel eine reelle Zahl zu, die einen Drehpunkt auf einer orientierten
Geraden mit dem Richtungswinkel festlegt. (Siehe die Pdf-Datei ' Die Drehpunktfunktion'). In
den folgenden Zeichnungen liegt die Spitze des Pfeils auf dieser Geraden bei '1' und seine Mitte bei '0'. Es
ist , wenn der Nullpunkt der Geraden g(0°) im Urspung einer komplexen Ebene liegt.
Für eine differenzierbare Funktion f ist und ist Tangente an die Kurve der
Drehpunkte. Zum Zeichnen der Kurve nach der Gärtner-Methode muss zu jedem Richtungswinkel ein
Winkel gefunden werden, so dass die Geraden und sich in einem Punkt P schneiden, der
folgende Eigenschaft hat:

Wenn man von der Summe der Abstände und die Länge des Wegstücks auf der
Drehpunktkurve zwischen und abzieht, ergibt sich für alle die gleiche Konstante c.
Im Folgenden wird gezeigt, dass dies mit der Gleichung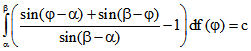
äquivalent ist, falls f im Intervall monoton ist.

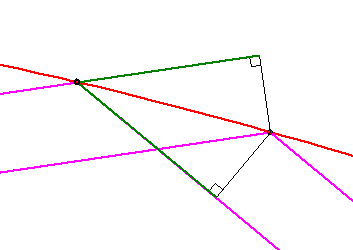
Die Drehpunkt-Funktion ist hier . Die blaue Drehpunktkurve ist eine
Spitzen-Evolvente einer Astroide. Die magentafarbenen Verbindungsstrecken von P mit und
wurden in gleicher Farbe zu einem geschlossenen Seil ergänzt. Es hat entsprechend der Gärtner-Methode
für alle Punkte P stets die gleiche Länge. Die rote Spur von P erfüllt dann die Billard-Bedingung.

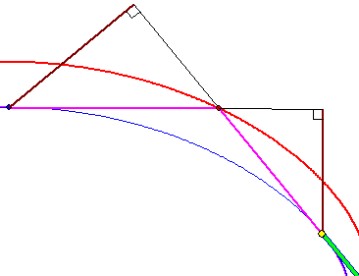
Die Abbildung zeigt einen Ausschnitt der roten
Billard-Kurve, die mit Hilfe der Gärtner-
Methode mit dem magentafarbenen Seil
erzeugt wurde. Das Seil wird in zwei
Stellungen gezeigt, die so nahe beieinander
liegen, dass entsprechende Seilabschnitte
fast parallel sind. Dann sind die beiden
grünen Strecken nahezu gleich lang, da die
Gesamtlänge des Seils gleich bleibt. Folglich
bilden diese Strecken mit der roten Kurve
nahezu gleich große Winkel. Die Abweichung
strebt gegen Null, wenn der Abstand der
roten Punkte gegen Null strebt.
Daraus folgt die Billard-Eigenschaft.

Der Verbindungsvektor des gelben Punktes und
des blauen Punktes wird mit der Drehpunkt-
Funktion f durch 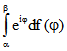bestimmt. ist der
Richtungswinkel der Tangente in .
Darum ist der Imaginärteil 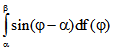von
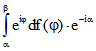der Abstand des Punktes von
. Der rote Punkt P hat darum von den
Abstand 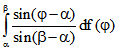. Analoges gilt für den
Abstand P von . Die Länge des Weges zwischen
und auf der blauen Kurve ist ,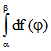
falls f hier monoton ist. Zieht man darum diese Länge
von der Summe der Abstände P von und
ab, so ergibt sich
.

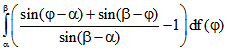Die Drehpunkt-Funktion ergibt eine Astroide als Drehpunktkurve. Die
Gärtner-Methode erzeugt auch hier eine Kurve, für welche die Billard-Bedingung erfüllt ist,
obwohl f nur zwischen benachbarten Spitzen monoton ist. Das Seil muss allerdings zwischen
den Spitzen springen.