Es lebe die Geometrie!

Kreise auf der Halbkugel

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Im Halbkugel-Modell der hyperbolischen Geometrie sind die 'Punkte' (H-Punkte) die Punkte
der Halbkugelfläche (mit dem Radius 1) mit Ausnahme des Randes und die 'Geraden' (H-Geraden)
die Halbkreise, welche senkrecht auf dem Rand enden. Anders als in der elliptischen Geometrie, in der
man Großkreise mit dem Kugel-Zentrum als Mittelpunkt betrachtet, sind diese 'Geraden' keine Geodäten.

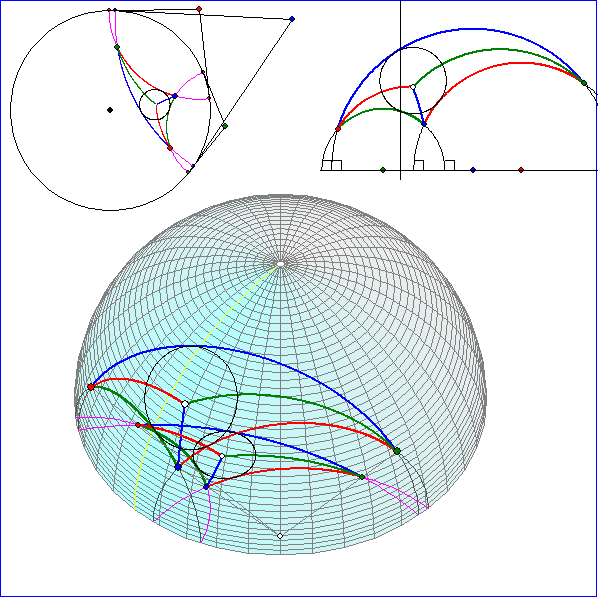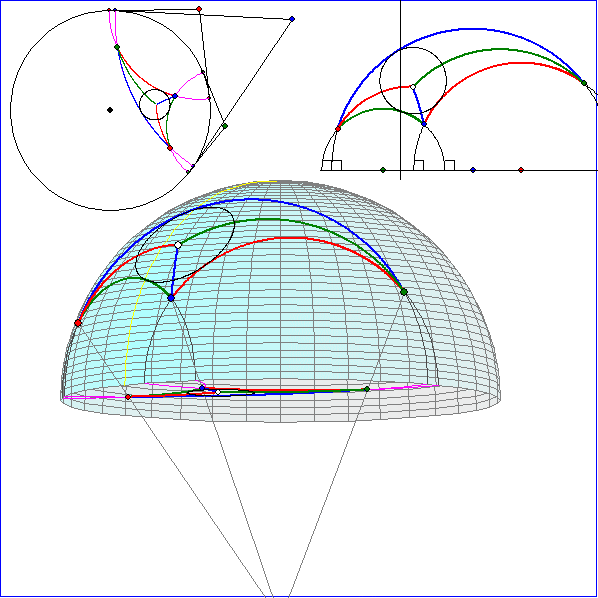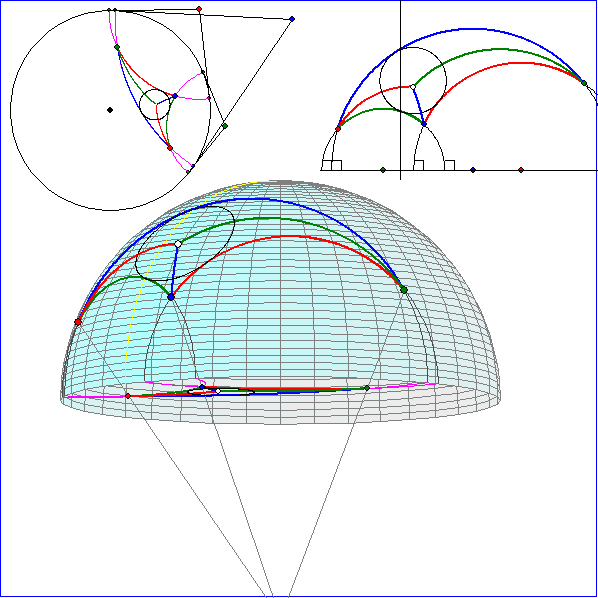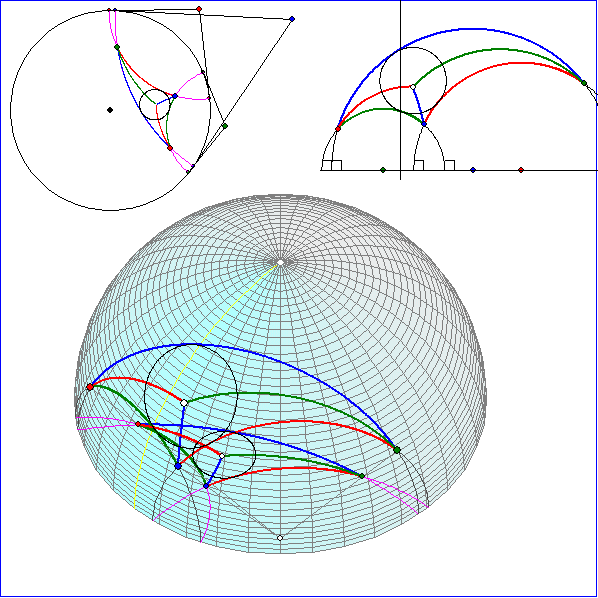
Die Animation zeigt ein Dreiseit aus H-Geraden mit H-Winkelhalbierenden und dem zugehörigen
H-Inkreis. Der H-Inkreis ist ein euklidischer Kreis, der die drei euklidischen Halbkreise des H-Dreiseits
berührt. Das Dreiseit wurde mit einer Zentralprojektion mit dem Zentrum in Punkt (0 ; 0 ; -1) auf die
x-y-Ebene projiziert (stereographische Projektion). Dabei werden euklidische Kreise in euklidische
Kreise abgebildet, und die Winkel zwischen den Kreisen in der Ebene und die entsprechenden Winkel
auf der Halbkugel stimmen in ihrer euklidischen Größe überein.

Das Bild in der x-y-Ebene ist oben links ohne perspektivische Verzerrung angegeben. Es stellt das
Kreis-Modell von Poincare dar. Oben rechts ist das Halbebenen-Modell von Poincare angegeben,
das sich durch stereographische Projektion der Halbkugel auf die Ebene x = 1 ergibt, wobei das Zentrum
der Punkt (-1 ; 0 ; 0) ist.

Die Abbildung deutet eine Lösung eines berühmten Problems aus der Antike an, das der große griechische
Mathematiker Apollonios von Perge (ca. 262 v. Chr. - ca. 190 v. Chr) gestellt hat. Es besteht darin, zu drei
vorgegebenen Kreisen K1, K2 und K3 einen Kreis K4 zu konstruieren, der alle drei Kreise berührt. Dazu ist der
Text von Apollonius ist nicht überliefert. Francois Viete (Vieta) (1540-1603), Carl Friedrich Gauß (1777-1855)
und Joseph Gergonne (1771-1859) haben das Problem auf unterschiedliche Weise bewältigt.

Wenn K1, K2 und K3 sich paarweise schneiden und es einen Kreis K0 gibt, der orthogonal zu allen drei
Kreisen ist, gelingt im Kreis-Modell von Poincare eine Lösung, weil die Kreisbögen im Innern von K0 dann
ein hyperbolisches Dreiseit bilden. Dazu können die hyperbolischen Winkelhalbierenden konstruiert werden.
Es sind dies Kreisbögen orthogonal zu K0, die die euklidischen Innenwinkel-Größen des Dreiseits halbieren.
Diese Winkelhalbierenden schneiden sich in einem Punkt D, welcher das hyperbolische Inkreis-Zentrum ist,
das sich vom euklidischen Inkreis-Zentrum unterscheidet. Um den Inkreis zu zeichnen, muss man von D aus
die hyperbolischen Lote auf K1, K2 und K3 fällen. Dies sind Kreisbögen durch D, die orthogonal zu K0 und
K1 bzw. K2 bzw. K3 sind. Der gesuchte Kreis geht durch die drei hyperbolischen Lotfußpunkte.

Das Bild zeigt das hyperbolische Dreiseit nach dem Kreis-Modell von Poincare zusammen mit dem
entsprechenden Dreiseit im Beltrami-Klein-Modell. Die K-Geraden im Klein-Modell sind Sehnen von
K0, deren Enden mit den zugehörigen Kreisbögen des Modells nach Poincare übereinstimmen. Von
einem K-Punkt P gelangt man zu dem entsprechenden Punkt P' des Kreis-Modells von Poincare, indem
man den K-Mittelpunkt von P mit dem Zentrum von K0 konstruiert. Die hyperbolische Größen derWinkel
bei P sind nach der Definition des Winkel-Maßes im Klein-Modell gleich den euklidischen Größen der
entsprechenden Winkel bei P'.