Es lebe die Geometrie!

Verschiedene Dreiseite mit gleichen Eckpunkten

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

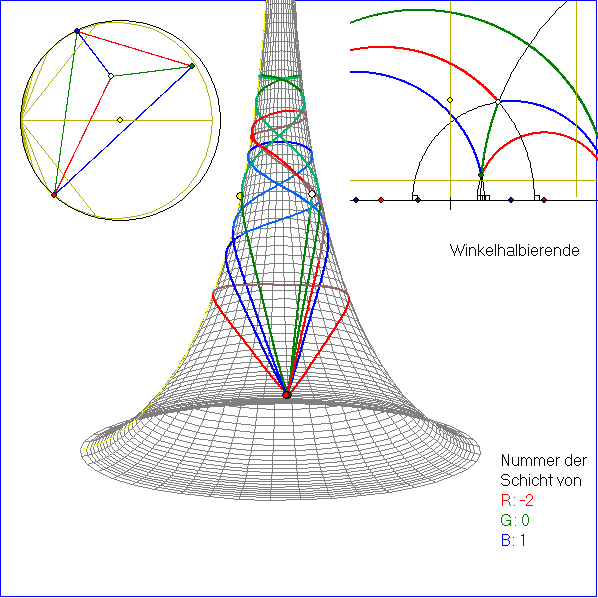
In den Bildern der Bildfolge werden 20 verschiedene Dreiseite mit den gleichen Eckpunkten R, G und B
dargestellt. Die kartesischen Koordinaten (x;y) sind (0,1 ; 0,1), (0 ; 0,8) und (0,7 ; 0). Dass unterschiedliche
Verbindungen durch Geodäten möglich sind, drückt sich darin aus, dass man diese Eckpunkte verschiedenen
Schichten der zur Pseudosphäre gehörenden riemannschen Fläche zuordnen kann. Je nach Schichtnummer
ist das Bild im Klein-Modell oben links ein unterschiedlicher Punkt. Und jedes der Dreiseite aus Strecken
innerhalb der gelb-grau gezeichneten Grenz-Ellipse gehört zu einem Geodäten-Dreiseit auf der Pseudosphäre.
Diesen Dreiseiten entsprechen im Poincare-Modell oben rechts durch Kreisbögen gebildete Dreiseite mit Zentren
auf der Rechtsachse. Hier stimmen im Unterschied zum Klein-Modell die Winkel mit denen auf der Pseudospäre
überein. Wenn r die Schichtnummer von R ist und g die von G, dann gibt der Betrag von g - r die Anzahl der
Punkte des gelben Null-Meridians an, die auf der Geodäte zwischen R und G liegen.

Seiten- und Winkelhalbierende haben stets einen gemeinsamen Schnittpunkt im Innern des Dreiecks. Wenn zwei
Höhen oder Mittelsenkrechte einen Schnittpunkt haben, dann liegt er auch auf der dritten. Während aber im
Klein-Modell Höhen und Mittelsenkrechte stets einen Schnittpunkt haben, fehlen diese im Poincare-Modell
und auf der Pseudosphäre zum Teil. Den Schnittpunkten, die im Poincare-Modell unterhalb der gelb-grauen
Parallelen zur Rechtsachse liegen, haben keine Entsprechung auf der Pseudosphäre, da die Geodäten am Rand
der Fläche enden, bevor es zum Schnitt kommt.

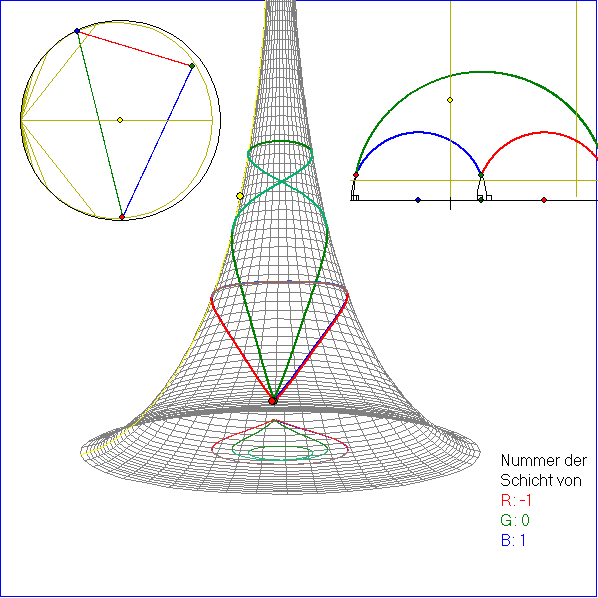
In dieser Bildfolge wird ein Dreiseit dargestellt, das nur einen Eckpunkt hat, nämlich den Punkt (0 ; 0,8 ; f(0,8)).
Er liegt allerdings in drei verschiedenen Schichten der zugehörigen riemannschen Fläche. Die Anzahl der
Seiten-Geodäten stimmt mit der Anzahl der Differenz-Beträge der Seitennummern überein. Auch hier haben
Seitenhalbierende, Winkelhalbierende und Höhen jeweils einen gemeinsamen Punkt. Die Mittelsenkrechten
liegen auf Meridianen der Pseudosphäre und haben einen gemeinsamen unendlich fernen Punkt auf der z-Achse.