Es lebe die Geometrie!

Ellipsen und analog konstruierte Kurven

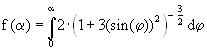, also
f ist die Drehpunktfunktion für die blaue Kurve und f ' die für die orangefarbene. Der zur Kurve gehörige
Pfeil dreht sich beim Zeichnen um einen Punkt auf der Geraden durch den Pfeil. Der Funktionswert gibt
den signierten Abstand des Drehpunktes von der Pfeilmitte an. (Der signierte Abstand ist von der Pfeilmitte
aus gesehen in Pfeilrichtung positiv und in der entgegengesetzten Richtung negativ.) Falls die Drehpunkt=
funktion in einem Intervall [a,b] monoton ist, gibt der Betrag der Differenz der Funktionswerte zu a und b
die Länge des Kurvenstücks zwischen den zu a und b gehörigen Punkten an. Der Drehpunkt auf dem
orangefarbenen Pfeil, der zur Ableitung f ' gehört, ist der Mittelpunkt des Schmiegkreises der blauen Kurve
zum Drehpunkt auf dem blauen Pfeil. Die orangefarbene Kurve ist also die Evolute der blauen Kurve, d. h.
die blaue Kurve ist Evolvente der orangefarbenen. Die blaue Kurve wird beschrieben durch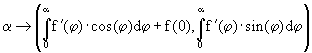
oder in komplexer Schreibweise durch .
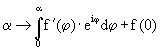Hierbei wurde die Mitte des Startpfeils als Koordinatenursprung gewählt. Entsprechend ist die orangefarbene
Kurve durch 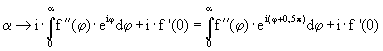gegeben. C gibt dabei den Kurvenpunkt für a = 0
an. Für die oben angegebene Funktion f ist die blaue Kurve eine Ellipse und ihre Evolute eine gestauchte Astroide.
In einer Darstellung ohne Integralzeichen ist .

Hier wird zusätzlich zur dunkelblauen Ellipse und iher Evolute die hellblaue Spur der Mitte des blauen
Pfeils gezeichnet. Die hellblaue Kurve wird beschrieben durch die Kurvenfunktion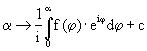
oder in komplexer Schreibweise durch .
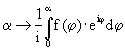Sie ist Evolvente der Ellipse, folglich ist die Ellipse ihre Evolute.

f(a) = 0,1a
Wenn die Drehpunktfunktion f wie hier eine lineare Funktion ist, ergibt sich als zugehörige Kurve ein Kreis.
Die hellblaue Kurve ist eine Kreisevolvente.

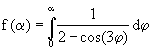, also
Die Ersetzung des Teilterms cos(2j) bei der Drehpunktfunktion der Ellipse durch cos(3j) führt zu einer
entsprechenden Kurve mit je drei Krümmungsmaxima und Krümmungsminima und sechs Sxmmetrieachsen.
Ohne Integralzeichen kann man f folgendermaßen beschreiben:

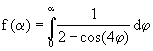, also
Die Ersetzung des Teilterms cos(2j) bei der Drehpunktfunktion der Ellipse durch cos(4j) führt zu einer
entsprechenden Kurve mit je vier Krümmungsmaxima und Krümmungsminima und vier Sxmmetrieachsen.
Ohne Integralzeichen kann man f folgendermaßen beschreiben: