Es lebe die Geometrie!

Das Berührungsproblem von Apollonios

Das Berührproblem von Apollonios von Perge (ca. 262 v. Chr. - ca. 190 v. Chr) besteht darin, zu
drei Kreisen in der Ebene einen vierten Kreis zu konstruieren, der alle drei Kreise berührt. Dies soll
auf dieser Seite über eine Laguerre-Spiegelung gelöst werden. In der folgenden Gleitschau wird dazu
erst die Bedeutung des Berührens für die Zylinder-Ellipsen dargestellt, deren Bilder bei der Blaschke-
Abbildung zu den vier Kreisen gehören. In der daran anschließenden Animation wird die Wirkung der
Verschiebung des Fixpunktes A einer Laguerre-Spiegelung auf ein Paar berührender Zylinder-
Ellipsen und der zugehörigen Zykeln untersucht.

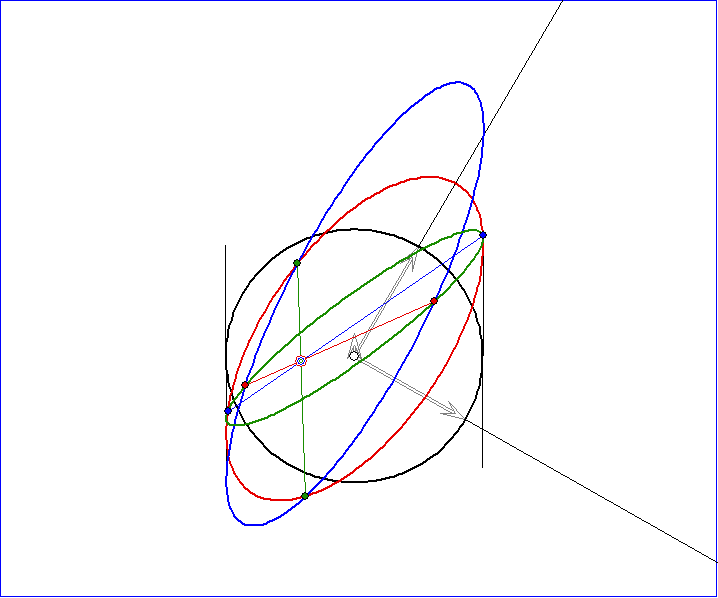
Das erste Bild der Gleitschau zeigt Zylinder-Ellipsen D*, E* und F* . Die Verbindungs-Strecken der
Schnittpunkte zu den drei Ellipsen-Paaren D*, E* und E*, F* und F*, D* sind in der jeweils dritten
Farbe eingezeichnet. Da sie auf den Schnittgeraden der zugehörigen Ebenen liegen, treffen sie sich in
dem dreifach eingekreisten Schnittpunkt C0 der drei Ebenen. C0 liegt im Innern des Zylinders. Im
2., 3. und 4. Bild wurden zwei Zylinder-Ellipsen B1* und B2* zugefügt, die D*, E* und F* berühren.
Das 5. Bild zeigt B1* zusammen mit den Dreieck der Tangenten in den drei Berührpunkten, das 6.
das Entsprechende für B2* , und das 7. Bild zeigt beide Dreiecke. Jede Seite dieser beiden Dreiecke
gehört zu der Geraden, in der sich die Ebenen der Ellipsen schneiden, die sich in dem zugehörigen
weiß gefüllten Punkt berühren. Die Berühr-Seite zu D* und B1* ist rot gezeichnet, entsprechend die
anderen Berühr-Seiten. Jeder Eckpunkt der Dreiecke ist in der dritten Farbe zu den beiden Farben
der Berühr-Seiten gezeichnet, die sich im Eckpunkt treffen. Er ist der Schnittpunkt der Berührellipsen-
Ebene des Dreiecks mit den Ebenen, die zu den Farben der beiden Berühr-Seiten gehören. Die
Schnittgerade dieser beiden Ebenen geht durch C0. Da dies für beide Dreiecke gilt, sind gleichfarbige
Eckpunkte dieser Dreiecke kollinear mit C0 und auch kollinear mit dem gleichfarbigen Schnittpunkten
der Zylinder-Ellipsen D*, E* und F* . Das 8. Bild verdeutlicht dies ohne Ellipsen.

Im 9. bis 12. Bild wurden die Verbindungsstrecken entsprechender Berührpunkte von B1* und B2*
eingezeichnet. Sie gehen bemerkenswerter Weise ebenfalls durch C0. Denn die Laguerre-Spiegelung
an C0 bildet die Punktmengen von D*, E* und F* jede auf sich ab und die von B1* in die von B2*.
Das 13. Bild zeigt alle Strecken ohne Ellipsen, im 14. Bild das Gleiche in einer anderen Perspektive.
Im 15. bis 17. Bild wird der Zusammenhang der Berührpunkte mit Zykeln der Blaschke-Abbildung
verdeutlicht. Dabei ist die Ursprungsgerade h durch C0 als magentafarbene Strecke angegeben. Die
beiden darauf markierten Punkte A0 und B0 spielen im Folgenden eine Rolle als Spiegelungs-Zentren.
Die zweite magentafarbene Gerade g ist nullpolar zu h. Das 18. Bild zeigt die Bild-Zykeln von D*, E* ,
F* , B1* und B2* der Blaschke-Abbildung zusammen. Das letzte Bild aus der Vogel-Perspektive
lässt einen Satz der ebenen Dreiecks-Geometrie erkennen.

Der Fixpunkt A der Laguerre-Spiegelung befindet sich zu Beginn der Animation am
Anfangspunkt der magentafarbenen Strecke von A0 nach B0 mit dem dreifach umrandeten
Punkt C0. Diese Strecke liegt auf der Ursprungsgeraden h, zu der die nullpolare Gerade g
die Zykelachse der Laguerrespiegelung ist. Den Punkt A0 muss man sich unten rechts hinter
dem durch zwei Parallelen zur z-Achse angedeuteten Zylinder vorstellen. Die Spiegelung bildet
ein Paar berührender Zylinder-Ellipsen D und B1 (blau und violett) in die blass gezeichneten
Ellipsen D* und B1* ab. Die Berührung von D und B1 bedeutet, dass die Ebenen zu D und B1
sich in einer Geraden schneiden, die den Zylinder berührt. Der Punkt C0 liegt auf D*, und
zwar nicht nur im Anfangsbild, denn D* und B1* werden nicht verückt. Der Ursprung des
Koordinatensystems liegt zu Beginn der Animation auf der Ebene zu D , was auch an der Lage
eingezeichneten Nebenachse der Ellipse erkennbar wird.

Zu den Ellipsen D , B1 , D* und B1* gehören die Zykel ZD , ZB1 , ZD* und ZB1* . Die
letzten beiden sind ebenfalls blass gezeichnet. Im Anfangsbild ist ZD ein Nullzykel und wird als
eingekreister blauer Punkt MD1 dargestellt. 'Berührung' bedeutet hier, dass der Punkt auf ZB1
liegt. Die gemeinsamen Tangenten von ZD , ZB1 und von ZD* , ZB1* schneiden sich auf der
Achse g im Punkt P.

Im Laufe der Animation wird A auf h in Phase 1 zunächst nach C0 bewegt. Bei festgehaltenen
Ellipsen D* und B1* werden dabei ihre Spiegelbilder D und B1 verrückt, wobei die Berührung
erhalten bleibt. Der Berührpunkt Q der Zykel ZD und ZB1 bewegt sich dabei auf dem Kreis K
um P durch den anfänglichen Nullzykel-Punkt MD1. Die Mittelpunkte von ZD und ZB1 bewegen
sich auf Lotgeraden LD und LB von g. Wenn Q den violett eingekreiste Schnittpunkt MB1 von LB
und K passiert, wird ZB1 zum NullZykel und wechselt danach die Orientierung. Das gleiche geschieht
beim Durchlaufen des zweiten Schnittpunkts MB2 von LB und K. Wenn A in C0 angekommen
ist, fallen ZD und ZD*, sowie ZB1 und ZB1* zusammen, da dann A auf der Ebene zu D* liegt.

In Phase 2 wird der Berührzykel ZB1* von ZD* durch den Berührzykel ZB2* von ZD* ersetzt,
der seinen Mittelpunkt ebenfalls auf LB hat, aber ZD* in dem zweiten Schnittpunkt von ZD* und
K berührt. Dann bewegt sich A weiter von C0 nach B0. Bei Ankunft in B0 ist dann das Spiegelbild
ZD von ZD* zu einem Nullzykel im Schnittpunkt MD2 von K und LD geschrunpft, weil dann die
Ebene zur Ellipse D durch den Ursprung geht, wie auch schon zu Beginn von Phase 1. Auch bei
dieser Bewegung verlässt der Berührpunkt nicht den Kreis K und der Mittelpunkt von ZD bzw.
ZB2 nicht seine Lotgerade von g.

In den Phasen 3 und 4 werden die Bewegungen der Phasen 2 und 1 umgekehrt, wobei die Zykeln
ZD und ZB1 bzw. ZB2 um die zugehörigen Kegel ergänzt werden. Anschließend werden die vier
Phasen aus der Vogelperspektive wiederholt.

Die Bilder der Gleitschau nach der Animation zeigen Standbilder daraus. Zur Wiederholung der
Phasen 1 bis 4 aus der Vogelperspektive wurden die Tangenten vom Projektionsbild von A0 an
den Einheitskreis zugefügt, in dem die xy-Ebene den Zylinder schneidet. Die Verbindungen der
Berührpunkte gehen dann durch das Projektionsbild von B0. Wenn man den Einheitskreis in
der xy-Ebene zur Darstellung eines Klein-Modells der hyperbolischen Geometrie nutzt, sind
darin die Spiegelungen an den Projektionsbildern von A0 und B0 vertauschbar und ihr Produkt
stimmt mit der Spiegelung an der Verbindungsgeraden dieser beiden Punkte überein. Man kann
diese Spiegelungen als Bilder der Projektion der Laguerre-Spiegelungen an A0 und B0 auf die
xy-Ebene parallel zur z-Achse betrachten. Diese beiden Laguerre-Spiegelungen sind ebenfalls
vertauschbar.

Im vorletzten Bild der Gleitschau sind die Zykeln ZD für mehrere Positionen des Laguerre-
Spiegelungszentrums A zusammengefasst gezeichnet. Daran zeigt sich deutlich die besondere
Rolle der Schnittpunkte MD1, MD2 von K und der Lotgeraden LD , die euklidisch spiegelbildlich
zu g liegen. Denn die Kreise der Zykel ZD gehören zum Kreisbüschel, das von den Nullkreisen zu
MD1 und MD2 erzeugt wird. Wenn und die Koordinatenpaare dieser beiden
Punkte in der xy-Ebene sind, dann gibt es zu jedem Kreis diese Büschels reelle Zahlen s und t, so
dass eine Gleichung des Kreise ist. Für
ergibt sich eine Gleichung der Zykel-Achse g in der Form . Wenn man
voraussetzt, dass s und t nicht beide gleich Null sind und ist, verschwinden die quadratischen
Summanden in der Gleichung nicht und es ergibt sich für eine Gleichung der Form
mit dem Kreisterm. Dabei
ist und . Der
Mittelpunkt (m;n) des zugehörigen Kreises liegt darum auf der Lotgeraden LD , aber nicht zwischen
MD1 und MD2 . Jeden dieser Kreisterme kann man als Linearkombination von zwei verschiedenen
beliebig vorgegebenen Kreistermen des Büschels darstellen, wobei man einen dieser beiden Terme
auch durch den Term von g ersetzen kann.

Das letzte Bild der Gleitschau zeigt, wie man die Nullkreise zu MD1 und MD2 geometrisch
konstruiert, wenn der Zykel ZD und die Zykel-Achse g gegeben sind.

Diese Animation zeigt, wie ein gemeinsamer Berührzykel zu drei Zykeln ZD*, ZE* und ZF* mit Hilfe von
Laguerre-Spiegelungen entsteht. Die beiden Bilder der ersten beiden Stops verdeutlichen, wie man die
Zykel-Achse g konstruiert. Dabei ist vorausgesetzt, dass es zu jedem der drei Zykelpaar ZD*, ZE* und
ZE*, ZF* und ZF*, ZD* je zwei gemeinsame Tangential-Speere gibt. Für die zugehörigen Zylinder-
Ellipsen bedeutet dies, dass sich die drei zugehörigen Ebenen in einem Punkt C0 im Innern des Zylinders
schneiden. In der Zeichnung ist C0 dreifach umrandet markiert und liegt auf der Strecke zwischen
den Punkten A0 und B0, auf der die Zentren aller Laguerre-Spiegelungen liegen, die hier eine Rolle
spielen. Die Gerade h durch diese beiden Punkte geht durch den Ursprung und ist nullpolar zu g.
Die Pfeile der Tangential-Speere sind durch die Blaschke-Abbildung den Pfeilen zugeordnet, die zu
den Schnittpunkten der Geraden mit dem Zylinder gehören, in der sich die Ebenen je zweier Zylinder-
Ellipsen schneiden. Die Verbindungs-Strecken dieser Schnittpunkte zu den drei Ellipsen-Paaren
D*, E* und E*, F* und F*, D* haben den Punkt C0 gemeinsam. Da C0 auf h liegt, schneiden sich
die Tangential-Speere zu ZD*, ZE* bzw. ZE*, ZF* bzw. ZF*, ZD* auf der Zykel-Achse g.

Nach der Konstruktion der Zykel-Achse aus den Tangential-Speeren verlangt unser Verfahren
die Bestimmung der Nulkreise in dem Kreis-Büschel, das von ZD* und g bzw. ZE* und g bzw. ZF*
und g erzeugt wird. Das geometrische Verfahren ist im dritten Standbild der Gleitschau nach der
Animation dargestellt. In der Animation selbst wird in der ersten Pfase gezeigt, wie die Ausgangs-
Zykeln ZD*, ZE* und ZF* die Kreise der Kreis-Büschel bis zu den Null-Kreisen zu den umrandeten
Punkten MD1, ME1 und MF1 durchlaufen. Dabei wenden wir die Laguerre-Spiegelung auf ZD*, ZE*
und ZF* an, deren Zentrum A auf h markiert ist und sich ausgehend von C0 in Richtung A0 bewegt.

In der zweiten Phase wird der violette Zykel ZB10 durch MD1, ME1 und MF1 gezeichnet. ZB10 ist
der Berühr-Zykel der zugehörigen Null-Kreise. Da diese Null-Zykel Bilder der Laguerre-Spiegelung an
A0 von ZD*, ZE* und ZF* sind, ist der gesuchte Berühr-Zykel ZB1* von ZD*, ZE* und ZF* das Bild
von ZB10 bei der Spiegelung an A0. Die Animation zeigt einen Übergang von ZB10 nach ZB1* . Dabei
ist unterwegs der Berühr-Zykel ZB1 an den Zykeln ZD, ZE und ZF Bild von ZB1* bei Spiegelung an A.
Ein Zykel ZB1 entsteht also aus ZB10 durch Anwendung der Hintereinanderschaltug der Spiegelungen
an A und A0. Man kann sich dies als eine Art Verschiebung vorstellen. Bei diesem Prozess bleiben die
Mittelpunkte von ZD, ZE, ZF und ZB1 stets auf der gleichen Lotgeraden von g. Der Berührpunkt von
zum Beispiel ZB1 und ZD wird um den Schnittpunkt von g mit der Tangente an ZB10 im Punkt MD1
gedreht, bewegt sich also auf einem Kreis. Die entsprechenden Kreise zu ZE und ZF haben aber einen
unterschiedlichen Radius. Die Berührpunkte von ZD*, ZE* und ZF* mit ZB1* sind Schnittpunkte von
ZD*, ZE* und ZF* mit diesen Kreisen.

In den Phasen 3 und 4 werden die Phasen 1 und 2 für den zweiten Berührzykel ZB2* von ZD*, ZE*
und ZF* wiederholt.

In der Gleitschau wurde im Anschluss an die Standbilder der Animation in den letzten drei Bildern
die Lage der Kreise in der Vogelperspektive dargestellt. Das drittletzte Bild zeigt einen direkten Weg
zu den Berührkreisen, bei dem man die Laguerre-Spiegelungen beiseite lassen kann. Dazu konstruiert
man die Lote LD, LE und LF von den Mittelpunkten der Zykel ZD*, ZE*, ZF* auf die Achse g und
darauf wie im dritten Standbild der Gleitschau die umrandeten Punkten MD1, ME1 und MF1 , die zu
Nullkreise des von ZD* bzw. ZE* bzw. ZF* und g erzeugten Kreisbüschels gehören. Die Tangenten in
diesen Punkten an den Zykel ZB10 durch diese Punkte schneiden g in den Punkten AD, AE und AF.
Der Kreis mit dem Mittelpunkt AD, AE bzw. AFdurch MD1, ME1 bzw. MF1 schneidet dann ZD*,
ZE* bzw. ZF* in den Berührpunkten von ZB1* und ZB2* .

Im letzten Bild der Gleitschau sind zu den Zykel-Paaren ZD*, ZE* und ZE*, ZF* und ZF*, ZD* die
Potenzgeraden eingezeichnet, die sich auf der Lotgeraden LB im 'Potenz-Zentrum' schneiden. Dieses
Potenz-Zentrum ist Mittelpunkt eines Kreises, der ZD*, ZE* und ZF* orthogonal schneidet und dessen
Inneres damit die Punktmenge einer hyperbolischen Ebene im Poincare-Modell darstellt. Darin sind die
Kreise zu ZD*, ZE* und ZF* 'Geraden' des Modells und ZB1* gehört zum Inkreis des dadurch
bestimmten Dreiseits. Siehe dazu die Seite 'Kreise im Halbkugel-Modell'.

In dieser Animation durchläuft der hellgrüne Kreis das Kreisbüschel, das von den beiden
Nullkreisen zu den doppelt umrandeten Punkten MB1 und MB2 erzeugt wird. Wenn
bzw. das Paar aus den x- und dem y-Wert dieser Punkte ist, gibt es zu
jedem Kreis des Büschels (wie oben beschrieben) reelle Zahlen s und t, so dass zu dem Kreis
die Gleichung gehört. Wenn man
darauf verzichtet, auch die Achse g in dem Büschel zu erfassen kann man dabei
setzen.

Zu diesem Kreisbüschel gehören alle violett gezeichneten Kreise, die Achse g und auch der
schwarz gezeichnete Kreis um das Potenz-Zentrum von ZD*, ZE* und ZF*, der diese
Zykel orthogonal schneidet. Alle Kreise des Büschels sind (euklidisch) orthogonal zu jedem
Kreis mit dem Mittelpunkt auf g durch MB1 und MB2.