Es lebe die Geometrie!

Addition bei Tangenten-Pfeilecken

Wir untersuchen auf dieser Seite Tangenten-Vielecke von Drehpunktkurven. Dabei kommen zum Teil
Kurven mit Spitzen vor, in denen es keine eindeutige Tangente im üblichen Sinne gibt. Unter dem Begriff
'Tangente zum Richtungwinkel ' verstehen wir darum bei einer Kurve mit dem Richtungswinkel als
Parameter die gerichtete Gerade mit dem Richtungswinkel , die durch den Punkt mit dem Parameter-Wert
verläuft. Sie wird auch 'Stützgerade' genannt. Da auf den Seiten eines Tangenten-Vielecks dann eine
Richtung ausgezeichnet ist, sprechen wir von einem Tangenten-Pfeileck. Die hier betrachteten Pfeilecke haben
zwischen aufeinander folgenden Seiten stets einen gleich großen Winkel. Wenn bei einer Drehpunktkurve
alle Tangenten-Pfeilecke mit der Eckenzahl n und dem gleichen Winkel zwischen aufeinander folgenden
Seiten nur eine Seitenlänge vorkommt, nennen wir die Kurve n-Phil (-->Seite n-Phil).

Tangenten-Pfeilecke spielen bei der Addition von Drehpunktkurven aus folgendem Grund eine besondere
Rolle: Die Summe zweier Tangenten-Pfeilecke der Drehpunktkurven f und g (zu den gleichen Richtungen)
ist das Tangenten-Pfeileck der Drehpunktkurve zu f + g. Dies folgt daraus, dass sich der Punkt
durch Vektor-Addition der Ortsvektoren von und ergibt.

Darum ist die Summe zweier n-Phile ebenfalls ein n-Phil.

Wir untersuchen auf dieser Seite Tangenten-Pfeilecke von Drehpunktkurven, deren Drehpunktfunktion
Linearkombinationen der Funktion und solchen der Form
sind. Die zugehörigen Drehpunktkurven gehören zum Einheitskreis bzw. einer gedrehten {k;-k}-Zykloide.
Die {k;-k}-Zykloide gehört zu der Funktion . Die Ableitung nach
ergibt . Da der Ortsvektor des zugehörigen Punktes den Richtungswinkel hat,
hat folglich die {k ; -k}-Zykloide den Richtungswinkel als Parameter. Die zu der Drehpunktfunktion
gehörige Drehpunktkurve ist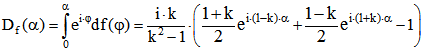
.
Darum ist .
Die Drehpunktkurve hat darum die gleichen geometrischen Eigenschaften wie die {k ; -k}-Zykloide.

Definiert man und , dann liegen die zugehörigen Punkte auf dem Kreis
um den Ursprung mit dem Radius . Wegen geht die Gerade g durch
P und Q auch durch den Zykloiden-Punkt . Aus folgt, dass g sogar
Tangente in ist. Wenn man den Richtungswinkel durch ersetzt mit einer ganzen
Zahl m und , dann ändert sich zwar Q, nicht aber P. Darum gehen alle
Tangenten in den Punkten durch P. Diese Tangenten sind die Parallelen zu den Seiten eines
regelmäßigen (k+1)-Ecks durch P. Für gehen entsprechend alle Tangenten in
durch Q. Es sind dies also die Parallelen zu den Seiten eines regelmäßigen (k-1)-Ecks durch Q.

Wir betrachten den (k+1)-fach belegten Punkt P als regelmäßiges (k+1)-Eck mit den oben genannten
Tangenten als Seitengeraden, wobei die Seitenlänge Null ist. Bei dieser Betrachtungsweise erscheint die
{k ; -k}-Zykloide als (k+1)-Phil , da bei allen diesen Tangenten-(k+1)-Ecken nur eine Seitenlänge
vorkommt, nämlich die Seitenlänge Null. Aus dem gleichen Grund ist die {k ; -k}-Zykloide auch
ein (k-1)-Phil.

Wenn oder mit natürlichen Zahlen r,s >1, dann bilden die Tangenten in
ein regelmäßiges t-Eck. Darum ist die {k ; -k}-Zykloide auch ein s-Phil.

In den sechs Perioden der Animation werden Drehpunktkurven dargestellt, für welche die Tangenten
in den Punkten zu den Richtungswinkeln für alle kongruente regelmäßige
Dreiecke bilden. Die Drehpunktkurven sind also Triphile (3-Phile). In der ersten Periode sind es die
Drehpunktkurven zu den Drehpunktfunktionen , und
. Die drei Tangenten haben jeweils einen gemeinsamen Punkt, so dass
die Seitenlänge des Tangenten-Dreiecks hier Null ist. Der gemeinsame Punkt liegt auf einer magentaroten
Kurve, die wir 'Spur des Zentrums' nennen. Sie ist bei f bzw. g ein Kreis vom Radius mit
k = 2 bzw. k = 4. Wenn eine Periode von 0 bis durchläuft, ist die Anzahl der Umäufe des
gemeinsamen Punktes bei f gleich 1+k, also 3, und bei g gleich 1-k, also -3. Bei h ergibt sich die Spur
des Zentrums durch Addition der Ortsvektoren von den gemeinsamen Punkten bei f und g unter
Berücksichtigung der unterschiedlichen Ursprünge. Da die Kreise zu f und g aber nicht den
Richtungswinkel als Parameter haben, ergibt sich die Zentrums-Spur nicht durch Addition dieser
beiden Kreise im Sinne der von uns benutzten Addition von Figuren. Dann wäre die Zentrums-Spur
von h ebenfalls ein Kreis. Da die Bewegung des gemeinsamen Punktes bei h durch Vektor-Addition
der gleichförmigen Kreis-Bewegungen der gemeinsamen Punkte bei f und g entsteht, und die
Winkelgeschwindigkeiten den gleichen Betrag, aber unterschiedliche Vorzeichen haben, ist die
Spur bei h eine Ellipse.

In der zweiten bis sechsten Periode der Animation wurde bei den Drehpunktfunktionen jeweils eine
Funktion hinzuaddiert mit einer Konstanten r, wobei der Zusammenhang h = f + g erhalten
blieb. Für jede der Drehpunktkurven bedeutet dies die Addition eines Kreises vom Radius r. Die
Tangentendreiecke zu den Richtungswinkeln haben dann alle r als Inkreisradius.
Die Drehpunktkurven sind darum alle Triphile. Dabei liegen diese Kurven genau dann im Innern der
Tangentendreiecke, wenn sie Ränder konvexer Mengen sind, also wenn die zugehörige Drehpunkt-
Funktion monoton ist. Das ist für h in der 5. und 6. Periode der Fall, für f und g nur in der 6.. Wegen
des Zusammenhangs h = f + g ist stets das Tangentendreieck zu h die Summe der Tangentendreiecke
von g und h. Die magentaroten Spuren des Zentrums der Dreiecke würden sich von Periode zu Periode
nicht ändern, wenn nicht der gemeinsame Maßstab der Drehpunktkurven von f, g und h geändert
werden müsste, um alle drei Kurven sichtbar zu halten.

In der Gleitschau im Anschluss an die Animation werden Standbilder davon gezeigt.

Die erste Periode der Animation zeigt, wie aus der roten Astroide durch Addition der grünen Kurve
die blaue Kurve entsteht, die eine Annäherung an die eine Kurve aus vier Kreisbögen darstellt, deren
Kreise schwarz eingezeichnet sind. Die Drehpunktfunktion der roten Kurve ist
und die der grünen
.
Die blaue Kurve wird exakt zur Kreisbogenkurve, wenn man das Bildungsprinzip des Terms von g bis
Unendlich fortgesetzt. Aus h wird dann

Dies ist eine Funktion, die bei der Fourier-Analyse des zweimaligen Umlaufes im Uhrzeigersinn mit konstanter
Geschwindigkeit um ein gleichseitiges Dreieck mit den Eckpunkten auftritt.
(Siehe https://www.vivat-geo.de/Pdf-Dateien/Fourierneck.pdf)
ist die stückweise lineare Funktion der y-Werte bei diesem Umlauf. Mit ist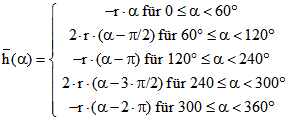


Die zugehörige Drehpunktkurve besteht aus je zwei Kreisbögen zum Radius r und 2r, die sich in den
Punkten , , und
berühren.

In der zweiten Periode der Animation wurde zu f und h der lineare Term hinzuaddiert. Für die
Drehpunktkurven bedeutet dies die Addition eines Kreise vom Radius r. Die rote Kurve wird dadurch
zu einer Evolvente der Astroide. Die blaue Kurve nähert sich dann einem Kreisbogen-Zweieck mit dem
Innenwinkel 60° an, dessen Drehpunktfunktion ist. Die Eckpunkte des Zweiecks
liegen bei (0 ; 0) und (0 ; 3r).

Bemerkenswert ist, dass alle Kurven Triphile sind. Zu f, g und h der ersten Periode und zu g der zweiten
Periode gehören Triphile mit Tangenten-Dreiecken zur Seitenlänge 0. Die Triphile von f und h in der
zweiten Periode haben lauter kongruente Tangenten-Dreiecke mit der Seitenlänge . Der Grund
dafür liegt darin, dass alle Summanden von die Form haben, wobei sich k um 1 von einem
ganzzahligen Vielfachen von 3 unterscheidet. Auch nach Addition des Kreise vom Radius r bleibt dieTriphil-
Eigenschaft erhalten, da alle Kreise Triphile sind.

Die Animation zeigt für das Pentaphil (5-Phil) den entsprechenden Zusammenhang wie in der
vorherigen Animation für das Triphil. In der ersten Periode wird zu der roten Drehpunktkurve mit
der Drehpunktfunktion die grüne Drehpunktkurve zur Drehpunktfunktion
addiert. Es entsteht die blaue
Kurve, die einem Kreisbögen-Zug angenähert ist. Dieser Zug ergibt sich exakt als Drehpunkt-
Kurve zur Drehpunktfunktion
. Dies ist
eine stückweise lineare Funktion, die bei der Fourier-Analyse des zweimaligen Umlaufes im
Uhrzeigersinn mit konstanter Geschwindigkeit um ein Pentagramm mit dem Zentrum (0 ; 0) und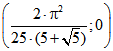
als Eckpunkt auftritt. Die Funktion gibt dabei die y-Werte an. Die sechs
Kreisbögen gehören paarweise zu den Radien

und es gilt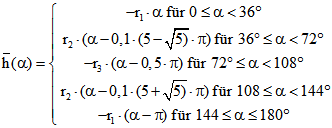

Auf dem Intervall ]180° ; 360°] setzt sich die Funktion periodisch fort.

Da in alle Summanden die Form haben, wobei sich k um 1 von einem ganzzahligen
Vielfachen von 5 unterscheidet, und die Drehpunktkurven dieser Summanden darum alle Pentaphile
sind, gilt dies auch für .

In der zweiten und dritten Periode der Animation wurde zu f und h der lineare Term hinzuaddiert.
Die Drehpunktkurve von wird dann zu einem Kreisbogen-Zug, der eine konvexe
Menge berandet. Zwei der Kreisbögen haben die Radien und vier die Radien . Für
zwischen 72° und 108° sowie zwischen 252° und 278° gibt es zwei Spitzen, da hier konstant ist.

In der dritten Periode der Animation wurden für die Pfeilecke die gleichen Tangenten benutzt, wie in
der zweiten, jedoch nicht die Schnittpunkte der Tangenten zu den Richtungswinkel und ,
sondern die zu den Richtungswinkeln und . Anstatt regulärer Fünfecke mit der
Überschlagungszahl 1 ergeben solche mit der Überschlagungszahl 2, also Pentagramme.